且SA=SB=SC,D为斜边AC中点

话题：且SA=SB=SC,D为斜边AC中点。（1）求证：SD垂直于面

问题详情：就是做SO垂直于ABC后怎么证明OA=OB=OC

回答：做SOABC于O 连接OA,OB,OC ∵SA=SB=SC OA=OB=OC O是底面ABC的外心即斜边AC中点D， O与D重合 SD垂直于面ABC 第二种 连BD,D为斜边AC中点BD=CD，△DSC为RT△且SDC为直角，△DSC和△BSD，∵SB=SC,BD=CD,SD=SD△DSC和△BSD全等 BDS和SDC=直角 ∵SDBD,SDAC SDABC

话题：如图所示,三棱锥S

回答：证明： 做辅助线，连接SD ∵ SB=AB,SC=AC,BC为公用边 △SBC ≌ △ABC （三边对应相等，两三角形全等） 得 SCB=ACB 又 SC=AC ，边CD公用 △SCD ≌ △ACD （两边一夹角对应相等，两三角形全等） SD=AD ， SDC=ADC 又 ADBC于D SDC=ADC=0 SDBC于D （不知道有没定理直接从 全等、ADBC 得到SDBC ，所以证明了一遍 ） 由 ADBC于D,SDBC于D ,AD、SD在平面SDA上相交于D 得 BC平面SDA （平面外的一条直线如果和这个平面内的两条相交直线都垂直， 那么这条直线就垂直于这个平面） BCSH （一条直线垂直于平面，则垂直平面内任意直线） 又 SHAD于H

话题：Rt三角形ABC所在平面外一点S,且SA=SB=SC,D为斜边AC

问题详情：Rt三角形ABC所在平面外一点S，且SA=SB=SC,D为斜边AC的中

回答：(1)易证△SAD≌△SBD≌SCD，SDA=SDB=SDC 在△SAC中，SDA=SDC=0则 SDA=SDB=SDC=0从而有SDDA,SDDC，即可证得SD垂直平面ABC。 (2)若AB=BC， （1）则SDBD,BDAC ，从而可得BD垂直平面SAC

话题：BD上的点,且（AM/ ）=(BN/ND),求证MN 平面SDC

问题详情：要有详细的过程

回答：连接AC交BD于O 在AC上取点E，使得AE/CE=AM/ 连接EN 所以EM‖SC（比例线段） 所以EM‖平面SDC 因为AC=2OE,BD=2OB 所以由AE/CE=AM/ 得AE/AC=AM/SA=BN/BD 所以AE/OA=BN/OB 所以EN‖AB‖CD 所以EN‖平面SDC 所以平面EMN‖平面SDC 因为MN在平面EMN内 所以MN 平面SDC

话题：三角形ABC是等腰直角三角形,斜边AC的长为10,S是三角形

回答：设D点为AC的中点，连接SD,BD， 因SA=SC，三角形SAC是等腰三角形，则SDAC，同理，BDAC， 三角形ABC是等腰直角三角形，BD是斜边AC 上的高，BD=1/2*AC=DC 三角形SDB和三角形SDC中，SD是公用边，DB=DC,SB=SC，三角形SDB全等于三角形SDC，角SDB=角SDC=0度，SDBD，前面有SDAC，因此SD平面ABC,SD即点D到平面ABC的距离，SB与平面ABC所成的角即角SDB. DC=1/2*AC=1/2*10=5 SC=13 则SD=（13^2-5^2）=12 sin角SDB=SD/SB=12/13

话题：四字成语造句

问题详情：抑扬顿挫 相依相随 焦躁不安 漫不经心 久别重逢 横遭不辛 震耳欲

回答：由于昨天跟一个老朋友久别重逢 所以写作业时漫不经心，今天要交作业时才想起有些是错的，可是已经交上去了心里焦躁不安，上课时被 骂得泣不成声

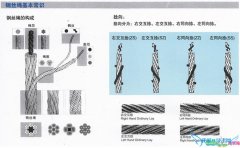
话题：常用SDC砂轮怎么标注？是什么意思？

回答：SDC砂轮就是金刚石砂轮，与CBN砂轮硬度差不多一般砂轮常用磨料A- 棕刚玉 WA- 白刚玉 C- 黑炭化硅 GC 绿碳化硅AC 混合磨料 SA- 单晶刚玉 MA- 微晶刚玉 BA- 黑刚玉 ZA- 锆刚玉PA- 铬刚玉 FA- 半脆刚玉 SG- 陶瓷刚玉 SC- 立方碳化硅 BC- 碳化硼 D- 金刚石

参考回答：SDC砂轮就是普通的金刚砂砂轮。金刚砂砂轮分两种一种就SDC另一种就是CBN。