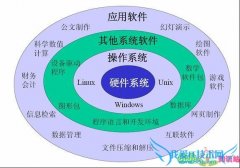
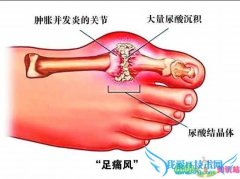
如图,P,Q是三角形ABC的边BC上的两点,且BP=PQ=QC=

话题：如图,P,Q是三角形ABC的边BC上的两点,且BP=PQ=QC=

回答：条件不够吧?

参考回答：∵PQ=AP=AQ ∴∠APQ=60 ∴∠APB=120 又∵BP=AP ∴∠ABP=∠PAB=(10-120)/2=30

话题：已知:如图,P,Q是三角形ABC 边上 BC上的两点,且BP=PQ=

回答：因为PQ=AP=AQ 所以三角形APQ是正三角形 所以∠APQ=∠AQP=60度 又因为BP=AP 所以∠B=∠BAP 而∠B+∠BAP=∠APQ=60度 所以∠B=30度 同理可得∠C=30度 所以∠BAC=10度-(∠B+∠C)=120度

话题：P,Q是三角形ABC 边BC上的两点,且BP等于PQ 等于AP等于

回答：解:因为AP=PQ=AQ, 所以△APQ是正三角形, 所以∠APQ=∠AQP=∠PAQ=60° 所以∠APB=10°-∠APQ=120° ∠AQC=10°-∠AQP=120°. 又因为BP=AP,AQ=QC, 所以△ABP≌△AQC,且都为等腰三角形. 所以计算可得∠ABP=∠ACB=30°. 因为△ABP≌△AQC, 所以AB=AC, 所以△ABC也是 等腰三角形, 所以∠BAC的度数=60+30+30=120度

话题：如图 已知PQ 三角形ABC的边BC上的两点,并且BP=PQ=QC

回答：角BAC度数为120度 由已知BP=PQ=QC=AP=AQ, 所以AP=AQ=PQ, 因此在三角形APQ中,三边相等,故三角形APQ为正三角形,所以角PAQ=60度, 有角APQ=60度,所以角APB为120度,在三角形ABP中,BP=AP,三角形为等腰三角形,所以角BAP=30度,同理可得角CAQ=30度, 综上所述,角BAC=120度

话题：如图测12

回答：角BAC度数为120度 由已知BP=PQ=QC=AP=AQ, 所以AP=AQ=PQ, 因此在三角形APQ中,三边相等,故三角形APQ为正三角形,所以角PAQ=60度, 有角APQ=60度,所以角APB为120度,在三角形ABP中,BP=AP,三角形为等腰三角形,所以角BAP=30度,同理可得角CAQ=30度, 综上所述,角BAC=120度

参考回答：因为BP=PQ=QC=AP=AQ,所以AP=PQ=AQ,三边相等,角PAQ.QPA.PQA=60°,因为BP=AP,角BPA=10°-60°=120°。三角形

话题：如图所示,点P,Q是三角形ABC中BC 边上 的两点,并且BP=

问题详情：若点M是 BC 边上 的一个动点,三角形ABM的面积是y,若CM=x,AP

回答：(1)全等 三角形有两对△ABP≌△ACQ,△ABQ≌△ACP(2)∵AP=AQ∴∠APQ=∠AQP∴∠APB=∠AQC∵PA=QA,PB=QC∴△APB≌△AQC(3)∵AP=PQ=QC∴△APQ是 等边三角形作AN⊥BC于N∵AP=2∴AN=√3,BC=3AP=6∴PM=6-x∴y=1/2(6-x)*√3∴y=(-√3/2)x+3√3

参考回答：1)ABQ=ACP,ABP=ACQ2)AP=AQ=PQ 所以APQ是 等边3角形,APQ=AQP=60,PC=BQ=2PQ,AQ=AP 所以APC=AQB(边角边)3)面

话题：已知P,Q是三角形ABC的边,BC上的两点,并且PB=PQ=

问题详情：要计算得过程诺!!!

回答：∵PQ=AP=AQ∴△APQ是 等边三角形∴∠APQ=∠AQP=∠PAQ=60°又PB=AP,QC=AQ,∴∠B=30°,∠C=30°∴∠BAC=10-30-30=120°

参考回答：∵PQ=AP=AQ∴△APQ是 等边三角形∴∠APQ=∠AQP=∠PAQ=60°又PB=AP,QC=AQ,∴∠B=30°,∠C=30°∴∠BAC=10-30-30=120°

话题：如图14,P,Q是三角形ABC的边BC上的两点,并且BP等于QC

问题详情：如图14,P,Q是三角形ABC的边BC上的两点,并且BP等于QC等于

回答：因为AP=PQ=AQ,所以△APQ是正三角形,所以∠APQ=∠AQP=∠PAQ=60°所以∠APB=10°-∠APQ=120°∠AQC=10°-∠AQP=120°.又因为BP=AP,AQ=QC,所以△ABP≌△AQC,且都为等腰三角形.所以计算可得∠ABP=∠ACB=30°.因为△ABP≌△AQC,所以AB=AC,所以△ABC也是 等腰三角形,所以∠BAC的度数=60+30+30=120度

参考回答：请给完整的题目

话题：如图,P,Q是三角形ABC的边BC上的两点,并且BP=PQ=

问题详情：如图,P,Q是三角形ABC的边BC上的两点,并且BP=PQ=QC=AP=

回答：中间三角形APQ是正三角形,角PAQ60度。俩边的 三角形都是 等腰三角形,所以2乘角BaP加上2乘角CaQ加加上角PaQ等于10度,得角PaQ加CaQ等于60°。所以角BaC等于120°

参考回答：要给出一个角的度数才好求啊。

话题：如图所示,p,q为三角形abc的边ab

回答：对于BC上任意一点R来说,△PQR的 长中,PQ 的长度始终没变,因此问题等价于在BC上求一点R,使PR+QR最小,这和那个课本上的建造自来水厂的问题一模一样。 作点P关于BC的对称点P',连结P'Q交BC于点R,则R是使△POQ 长最小的点。 设D是 BC上异于R的任意一点 ∵P、P'关于BC对称 ∴PR=P'R,PD=P'D 在△P'QD中,QD+P'DP'Q=P'R+QR ∴QD+PDPR+QR ∴PQ+QD+PDPQ+PR+QR 也就是,对于BC上异于R的任意一点D,都有△PQD的 长大于△PQR的 长 这说明△PQR的 长最小