数字信号处理实验五MATLAB

数字信号处理实验五

一、实验目的:

1、快速傅里叶变换并不是一种新的变换方法，它是计算DFT的一种有效算法。它是信号谱分析的有力工具。通过本次实验，学习使用FFT进行信号分析的方法，加深对FFT的理解；

2、理解FFT进行信号频谱分析可能出现的问题，如：频谱混叠，阑珊效应，频谱泄露等，以便在实际中正确处理。

二、实验要求与实验内容:

1、通过实际例子学习使用FFT分析信号的方法。

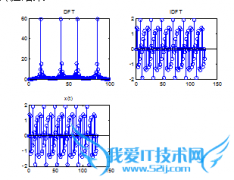
对信号x(t)=sin(2π×40t)+sin(2π×15t)进行DFT，对其结果进行IDFT，并将IDFT的结果和原信号进行比较（f=100Hz，n=128）。

2、通过采样点数的不同，了解对信号幅度谱的影响。

已知信号由15Hz幅值0.5的正弦信号和40Hz赋值为2的正弦信号组成，数据采样频率为100Hz，试分别绘制N=128点DFT的幅频图和N=1024点DFT幅频图。

3、编程实现对下列正弦信号的FFT分析，并讨论实验结果。

a.信号频率F=50Hz，采样长度N=32，采样时间T=0.000625s.

b.信号频率F=50Hz，采样长度N=32，采样时间T=0.005s.

c.信号频率F=50Hz，采样长度N=32，采样时间T=0.0046875s.

d.信号频率F=50Hz，采样长度N=32，采样时间T=0.004s.

e.信号频率F=50Hz，采样长度N=64，采样时间T=0.000625s.

f.信号频率F=250Hz，采样长度N=32，采样时间T=0.005s.

g.信号频率F=50Hz，采样长度N=32，采样时间T=0.0046875s.后补32个零做64点FFT。

4、例5-1、例5-2、例5-3。

三、实验结果与分析

Ⅰ

实验程序：

Fs=1/0.01;

figure(1);

subplot(221);

N=128;

n=0:N-1;t=0.01*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=sin(2*pi*40*t)+sin(2*pi*15*t);

y=fft(x,N);

stem(q,abs(y));

title('DFT')

subplot(222)

x1=ifft(y,N);

stem(n,x1);

title('IDFT')

subplot(223)

stem(n,x);

title('x(t)')

实验结果：

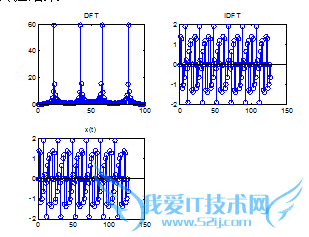
实验分析：原始信号与IDFT的信号相同

Ⅱ

实验程序：

Fs=100;

figure(1);

subplot(211)

N=128;n=0:N-1;t=0.01*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);

y=fft(x,N);

stem(n,abs(y));

title('128')

subplot(212)

N=1024;n=0:N-1;t=0.01*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);

y=fft(x,N);

stem(n,abs(y));

title('1024')

实验结果：

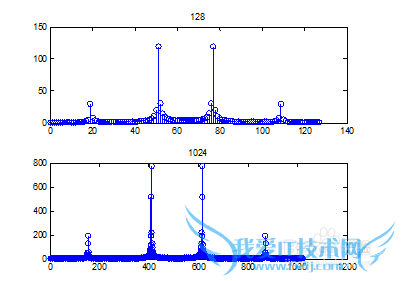
实验分析：图形的点数增加后的大体图像与点数少的相同，但是分辨率增加了。

Ⅲ

实验程序：

T=0.000625;

Fs=1/T;

figure(1);

subplot(221)

title('a');

N=32;n=0:N-1;t=T*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=sin(2*pi*50*t);

y=fft(x,N);

stem(q,abs(y));

title('a')

subplot(222);

T=0.005;

Fs=1/T;

N=32;n=0:N-1;t=T*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=sin(2*pi*50*t);

y=fft(x,N);

stem(q,abs(y));

title('b')

subplot(223);

T=0.0046875;

Fs=1/T;

N=32;n=0:N-1;t=T*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=sin(2*pi*50*t);

y=fft(x,N);

stem(q,abs(y));

title('c')

subplot(224);

T=0.004;

Fs=1/T;

N=32;n=0:N-1;t=T*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=sin(2*pi*50*t);

y=fft(x,N);

stem(q,abs(y));

title('d')

figure(2);

subplot(221)

T=0.000625;

Fs=1/T;

N=64;n=0:N-1;t=T*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=sin(2*pi*50*t);

y=fft(x,N);

stem(q,abs(y));

title('e')

figure(2);

subplot(222);

T=0.005;

Fs=1/T;

N=32;n=0:N-1;t=T*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=sin(2*pi*250*t);

y=fft(x,N);

stem(q,abs(y));

title('f')

figure(2);

T=0.0046875;

Fs=1/T;

N=64;n=0:N-1;t=T*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=sin(2*pi*50*t);

x1=[x(1:1:32),zeros(1,32)];

y=fft(x1,64);

subplot(223)

stem(q,abs(y));

title('g')

实验结果：

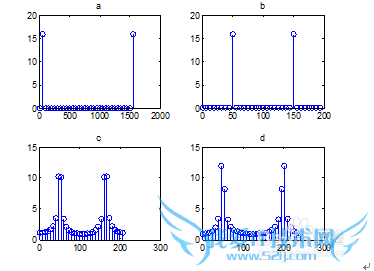
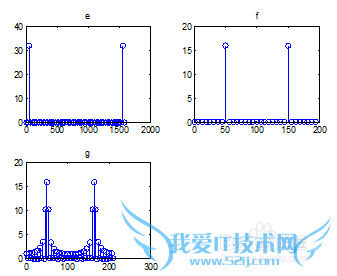
实验分析：通过计算r可以得知图形是否是发散的，c,d,g是发散的，其他的都是收敛的！

Ⅳ

例5-1、

实验程序：

%àyìa5-1

Fs=1/0.01;

figure(1);

N=50;n=0:N-1;t=0.01*n;

q=n*Fshttp://jingyan.baidu.com/article/N;

x=2*sin(4*pi*t)+5*cos(8*pi*t);

y=fft(x,N);

stem(q,abs(y));

title('FFT N=50')

figure(2)

subplot(221)

N=15;n=0:N-1;t=0.01*n;

q=n*2*pi/N;

x=2*sin(4*pi*t)+5*cos(8*pi*t);

y=fft(x,N);

stem(q,abs(y));

title('FFT N=15')

subplot(222)

N=25;n=0:N-1;t=0.01*n;

q=n*2*pi/N;

x=2*sin(4*pi*t)+5*cos(8*pi*t);

y=fft(x,N);

stem(q,abs(y));

title('FFT N=25')

subplot(223)

N=35;n=0:N-1;t=0.01*n;

q=n*2*pi/N;

x=2*sin(4*pi*t)+5*cos(8*pi*t);

y=fft(x,N);

stem(q,abs(y));

title('FFT N=35')

subplot(224)

N=55;n=0:N-1;t=0.01*n;

q=n*2*pi/N;

x=2*sin(4*pi*t)+5*cos(8*pi*t);

y=fft(x,N);

stem(q,abs(y));

title('FFT N=55')

实验结果：

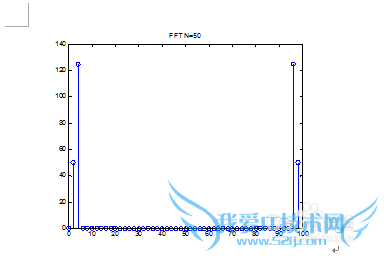
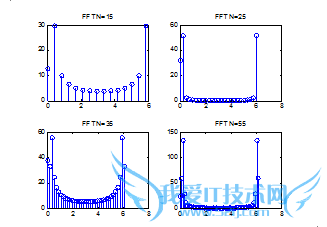
实验分析：N的取值决定了图形的分辨率

例5-2

实验程序：

%àyìa5-2

figure(1);

subplot(211)

N=64;n=0:N-1;t=0.01*n;

q=n*2*pi/N;

x=2*sin(4*pi*t)+5*cos(8*pi*t);

y=fft(x,N);

plot(q,abs(y));

title('FFT N=64')

subplot(212)

N=64;n=0:N-1;t=0.01*n;

q=n*2*pi/N;

x=2*sin(4*pi*t)+5*cos(8*pi*t)+0.8*randn(1,N);

y=fft(x,N);

plot(q,abs(y));

title('FFT N=64(with noise)')

实验结果：

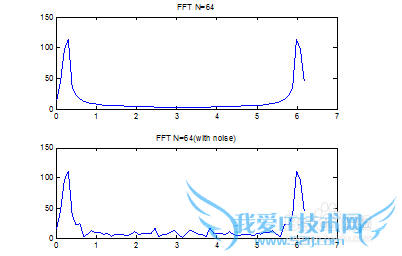
实验分析：这种噪声不会影响信号的检测！

例5-3

实验程序：

closeall;clf;

L=50000;

N=2*L-1;

n=1:L;

x1=0.5*n;x2=2*n;

t0=clock;

yc=conv(x1,x2);

tc=etime(clock,t0);

yf=ifft(fft(x1,N).*fft(x2,N));

tf=etime(clock,t0);

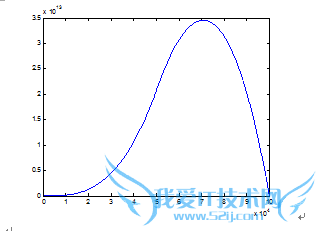
n1=0:length(yf)-1;

plot(n1,yc,'r');

figure

plot(n1,abs(yf),'b');

实验结果：

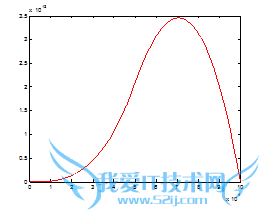
>> tc

tc=

11.7030

>> tf

tf=

11.8750

>> tf-tc

ans=

0.1720

实验分析：FFT的计算时间比conv函数快。

四、实验总结：

学会了Matlab分析快速傅立叶变换及其性质。理解了应用FFT进行信号频谱分析可能出现的问题。做实验时注意数字相乘和字母相乘需要加点，同时注意提前定义所有需要的基本扩展函数，做实验时需要仔细认真！

用户类似问题：

问题1：基于matlab的数字信号处理仿真实验平台

用matlab编写程序 >>详细

问题2：数字信号处理matlab实验，不知道如何回答下列问题...

(1) The uncorrupted signal s[n] is 2n(0.9^n) (2) The additive noise d[n] is a uniform distributed noise on the open interval (-0.4,0.4) (3) the relations between the signals x1, x2, x3, and the signal x : x1, x2, and x3 are dif... >>详细

问题3：Matlab数字信号处理…第五题啊 求程序 谢谢

你可以下载作业吧！ >>详细

问题4：数字信号处理matlab实验代码请教（紧急！可追加分数）

n=0:15; L=0:31; x=cos(5/16*pi*n); X_16=fft(x,16); X_32=fft(x,32); subplot(211); hold on; plot(n/16,abs(X_16),'r'); plot(L/32,abs(X_32)); hold off; w=linspace(0,pi,512); h=freqz(x,1,w); subplot(212); plot(w/pi,abs(h)); 我也是初... >>详细

问题5：数字信号处理 x(n)=u(n+5)-x(n-5)

不一定要用Matlab做，有解析解。 如果是DFT可以用Matlab来求解，但是问题本身应当先限定点数才对。 x(n) = u(n+5) - x(n-5) X(k)*(1+W(5k)) = U(k)*W(-5k) X(k) = U(k) * W(-5k)/(1+W(5k)), where U(k)=DFT(u(n)) is a sinc function, and W(k) ... >>详细