拉格朗日方程法建立多自由度振动系统运动方程

一、广义坐标

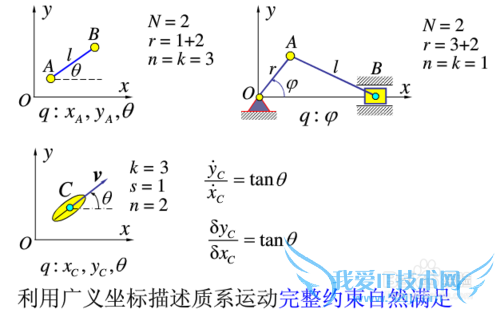
物体的机械运动规律可用不同的坐标系统表示，我们把秒速系统位形所需要的独立参数或独立坐标称为广义坐标，通常用q1,q2,q3,......qn表示，其中n为独立坐标个数。广义坐标具有以下几种性质：

1. 完备性：广义坐标可以确定系统任意时刻的位形和形状；

2. 独立性：同一组广义坐标之间相互独立、是线性无关的，之间互无函数关系；

3. 不唯一性：一个系统的广义坐标是不唯一的，但个数都等于系统自由度数，且都能用来描述系统的振动规律。

二、广义力

与广义坐标对应的是广义力，广义力是广义上的力，它的量纲有它与广义坐标虚位移的乘积为功的物理量纲决定的，即：若广义坐标为线位移，则广义力就是通常意义上的作用力；若广义坐标为角位移，则广义力就是力矩。

三、拉格朗日方程

根据拉格朗日理论可知，振动系统的运动方程可以用动能T、势能V和耗散能D表达成下图所示的表达式：

四、拉格朗日方程法的步骤

利用拉格朗日方程建立系统运动偏微分方程，可以避免未知约束反力的出现，简化推导过程，其解题步骤可归纳为：

(1) 首先判断系统的自由度数，并选取适当的广义坐标系；

(2) 以广义坐标和广义速度建立系统的动能T表达式；

(3) 当主动力是保守力，建立用广义坐标表示的只能U的表达式；

(4) 对于有阻尼情况，应该单独考虑阻尼，计算相应广义速度对应的耗散能函数D;

(5) 当有非保守力时，计算广义坐标qi对应的广义力Qi

(6) 将T、V、D和Qi ，代入拉格朗日方程进行运算，即可得到振动系统的运动偏微分方程。

五、算例分析

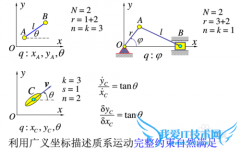
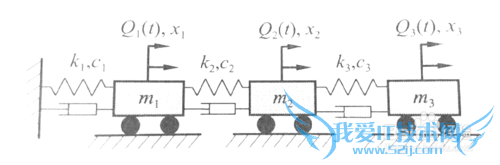
建立如下图1所示的三自由度质量-阻尼-弹簧振动系统的振动方程。

解：如图所示，建立坐标系，眼水平振动方向选择广义坐标系(x1,x2,x3),则按上节所述步骤，依次求解。求解过程如下图2所示。

用户类似问题：

问题1：已知两个自由度系统的拉氏量，求解运动方程、本征...

你的拉格朗日量确定是对的？计算的数字挺麻烦的，不太整，不过也有可能失我算错了，思路没问题，你最好验算一遍。具体过程如下： >>详细

问题2：拉格朗日方程（第二类）的三个形式，理论力学的，...

拉格朗日方程的一般形式是：   式中T为用各广义坐标qi和广义速度 qi导 表示的系统的动能；Qi为对应qi的广义力.方程式的个数等于系统的自由度N.保守系统中存在势函数V（q1,q2,…,qN；t),则广义力Q=?V/?qi,又因V中不含qi,V/?qi... >>详细

问题3：用拉格朗日力学推导两轮小车运动方程

看分析力学的教材吧 >>详细

问题4：拉格朗日方程适合的力学体系是哪些？有什么特点？...

你好 拉格朗日方法和欧拉方法一般是一起作对比出现的 拉格朗日方法着眼于个别质点运动，所以要求质点能够辨识，一般出流体以外的质点运动都用拉格朗日方法 欧拉方法着眼于一定空间内各个参数的变化，是场方法，一般用于流体研究。 两者具体的定... >>详细

问题5：拉格朗日

约瑟夫·拉格朗日（Joseph-Louis Lagrange，1736~1813）全名为约瑟夫·路易斯·拉格朗日，法国著名数学家、物理学家。1736年1月25日生于意大利都灵，1813年4月10日卒于巴黎。他在数学、力学和天文学三个学科领域中都有历史性的贡献，其中尤以数学方... >>详细