二叉树的定义及特征

树是一种数据结构,而二叉树是其中最容易并且应用非常广泛的一种.

一棵二叉树是由结点的有限集合组成,这个集合可以为空,那么称为空二叉树;也可以由一个根结点以及两棵不相交的左右二叉树组成,这两棵二叉树分别称为这个根结点的左子树和右子树.这两棵子树的根称为此二叉树根结点的子结点.从一个结点到其它两个子节点都有边相连,这个结点称为其子结点的父结点.

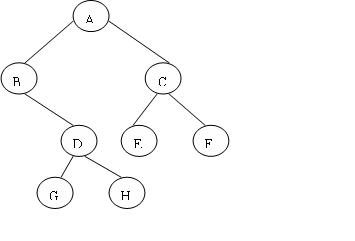
如果一棵树的一串结点N1,N2....Nk有如下关系:结点Ni是Ni+1的父结点(1<=i

结点M的深度就是从M结点到根结点的最短路径长度,即从根结点到M结点最短路径上的边数;而该结点的高度等于该结点作为根结点的二叉树到它的最长的一个叶结点的路径长度.那么叶结点的高一定等于0，而根结点的深度一定等于0，而根结点的高就等于树的高，叶结点的深也就等于树高.任何深度为d的结点层数为d,根结点层数为0,深度为0.那么说来,一个结点的深度,路径长度以及层数均相等.

没有非空子树的结点称为叶结点,即它不存在任何非空子结点.至少有一个非空子树的结点称为分支结点或内部节点,即一棵二叉树除了叶结点以外的所有结点均为分支或内部结点.

两种特殊的二叉树名称:

满二叉树:每一个内部结点或者是分支结点,恰好有两个非空子结点或叶结点.

完全二叉树:从根结点起每一层从左到右填充.一根高度为d的完全二叉树除了d-1层以外(即最高的这一层),每一层都是满的(即从第0层到d-2层是满二叉树),但d-1层的叶结点集中在左边的若干位置上.

从两者的定义可以看出，满二叉树只是完全二叉树的一种特例。即如果完全二叉树是一个集合A，那么满二叉树就是集合A的一个子集，因为我们可以把满二叉树看成是一个按从左到右结点都填满了的完全二叉树。

下面给出两个对于二叉树的定理:

满二叉树定理:非空满二叉树的叶结点数等于其分支结点数加一.

适用于所有二叉数的定理:一棵非空二叉树其空叶结点的数目等于其结点数目加一.

认真理解上面的所有定义,最好根据图形来分析.

本文来源 我爱IT技术网 http://www.52ij.com/jishu/1718.html 转载请保留链接。