java数据结构教程：回溯法求有向图的欧拉回路

【1】作品介绍：
如果可以“一笔画成”某个图形，这个图形就至少存在一条欧拉回路。画线的轨迹就是一条欧拉回路。一个图有多个欧拉回路。求有向图的欧拉回路，有很多算法，比如弗罗莱Fleury算法（这种算法可归结为“不走桥，除非无桥可走”，很容易实现），Fleury算法属于贪婪算法，不能求出某个有向图的全部的欧拉回路。使用回溯法求有向图的欧拉回路，可以求出某有向图的所有的欧拉回路。该作品是我重温《离散数学》之后，发现“求有向图的欧拉回路”是一个典型的可以使用“回溯法”的例子。就动手做了。
【2】运行效果：
五角星有多少一笔画成有多少方法？

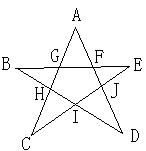
证明了：“考虑”五角星的特殊性，五角星共有96种“一笔画成”的画法，如果“不考虑”五角星是轴对称图形，这个数还应该要乘以2，如果“不考虑”五角星是特殊的中心对称图形（每旋转360／5度就和自己重合），这个数应该还要乘以5。
【3】程序亮点：
①“二叉树”类中，数据成员的命名与众不同。
public class BiTreeNode {
    public BiTreeNode eldership = null;
    public BiTreeNode child = null;
    public BiTreeNode brother = null;

    private Object data;
    //其他省略
    ……
}
这是程序中使用到的“二叉树”类，用来存储在搜索时形成的“树”。其中eldership是长辈的意思。这样命名充分体现了：我对“为什么要把树转化为二叉树？和“如何转化”这两个问题理解得很透彻。其最大的优点是：相当于给某节点的子节点编号了。
②解决了“图的存储”。
③解决了“搜索算法”这一关键算法。虽然这个算法在很多书中提到，但是具体地把它实现出来，需要考虑许多细节。
【4】不如意之处：
①没有将搜索引擎独立出来，回溯法总牵扯到一些固定的东西：扩展条件、回溯条件、结束条件。搜索引擎具有独立出来可能性。目前没有看到这方面的资料。我自己也没有深入研究过这个问题。  

本文来源 我爱IT技术网 http://www.52ij.com/jishu/309.html 转载请保留链接。