本文介绍使用Excel的规划求解模块解决一个简单的管理科学应用问题。
小明喜欢吃牛排和土豆,而且每天仅吃这两种食物。
每份牛排8元,每份土豆4元;
每份牛排含有碳水化合物5克、蛋白质20克;
每份土豆含有碳水化合物15克、蛋白质5克;
营养学研究表明每人每天至少需要碳水化合物50克、蛋白质40克;
问小明如何安排,在其营养有保证的前提下,使每天用餐的总花费最小?
(这个例子是虚构的,没有什么营养学依据)

前期准备工作(包括相关工具或所使用的原料等)
Excel 2010详细的操作方法或具体步骤
(1)建立模型结构
Exce软件的结构是行和列。
B列表是牛排的事;
C列表示土豆的事
D列表示实际摄入量;
F列表是营养最低要求;
第2行表示碳水化合物的事
第3行表示蛋白质的事
第4行表示单价的事
第5行表示数量的事
(2)输入已知条件
根据模型的行列设定,行和列交汇处的单元格就有了特定含义
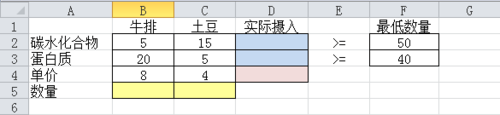
单元格【B2】就表示每份牛排含碳水化和物的数量,根据已知条件输入5;
单元格【B3】就表示每份牛排含蛋白质的数量,根据已知条件输入20;
单元格【B4】就表示每份牛排的价格,根据已知条件输入8;
--------
单元格【C2】就表示每份土豆中含碳水化和物的数量,根据已知条件输入15;
单元格【C3】就表示每份土豆中含蛋白质的数量,根据已知条件输入5;
单元格【C4】就表示每份土豆中的价格,根据已知条件输入4;
-------
单元格【F2】就表示每天每人最低需要的碳水化和物的数量,根据已知条件输入50;
单元格【F3】就表示每天每人最低需要的蛋白质的数量,根据已知条件输入40;
------
单元格【B5】就表示每份牛排的数量,自变量,无需输入;
单元格【C5】就表示每份牛排的数量;自变量,无需输入
(3)输入3个公式
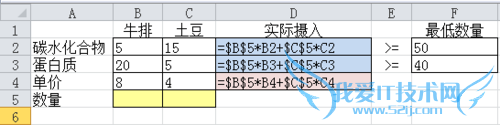
在单元格【D2】输入函数【=$B$5*B2+$C$5*C2】
因为自变量【$B$5】和【$C$5】总要用,所以是绝对引用
然后选中单元格【D2】,拖拽至【D4】
--------
更一般的方法是,在在单元格【D2】输入函数【=sumproduct($B$5:$C$5, B2:C2)】
因为自变量【$B$5:$C$5】总要用,所以是绝对引用
这种方法的好处是处理大模型——比如10行,8列的模型更有效率

(3)设置规划求解模块
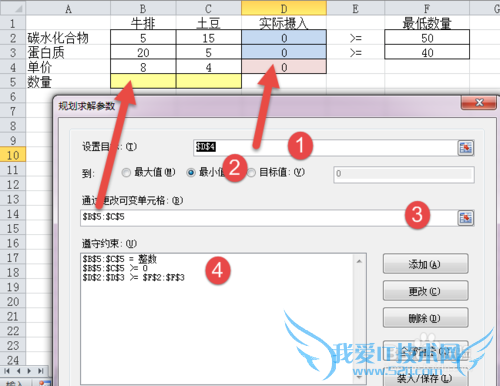
***点击【数据】——【规划求解】
***在弹出的窗口,【设置目标】,点击右侧的按钮,选中单元格【D4】——总利润
***其下,点选【最小值】——想求最小的总支出(与最大值问题有显著不同)
***其下,【可变单元格】点击右侧的按钮,选中区域【B5:C5】——两个自变量
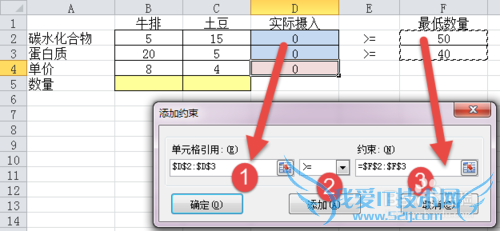
***在【规划求解】窗口,点击右侧的【添加】,添加3类约束条件
其一、实际摄入量>=最低需求(与最大值问题有显著不同)
其二、自变量(桌子、椅子数量的数量)>=0
其三、自变量(桌子、椅子数量的数量)是整数
***求解方法,点选【单纯线性规划】
0信息应用01: 加载Excel的规划求解模块
0信息应用02: Excel规划求解初步——最大值
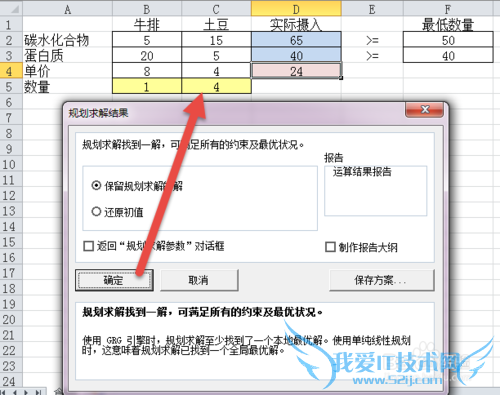
最优解如下
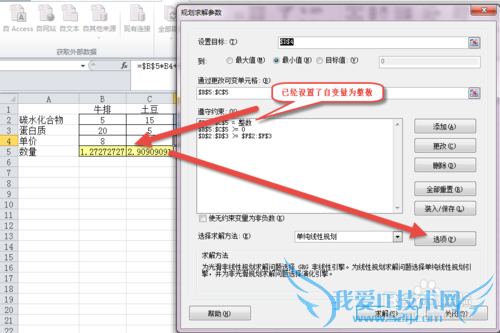
如果出现的最优解不是整数,解决方法是点击【选项】
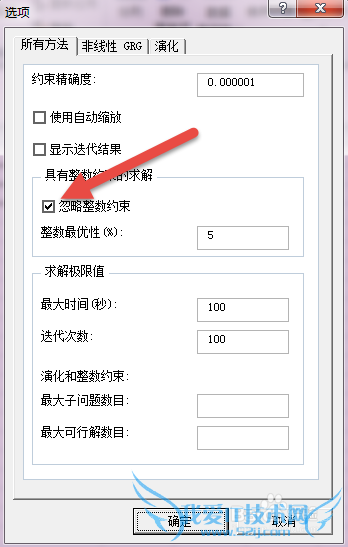
在弹出的窗口,确保【忽略整数约束】没有被选中——那么整数约束条件才有效,就可以解决问题了。
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
