本文介绍使用Excel的规划求解模块,解决服务设施定位的问题,在运筹学中被称为覆盖问题。
如下图所示,考虑满足条件(每个社区30英里范围内至少有一家诊所)的前提下,诊所总数越少越好。自变量是诊所的位置——对应九个社区的9个二分变量(0表示不设诊所,1表示设诊所)。
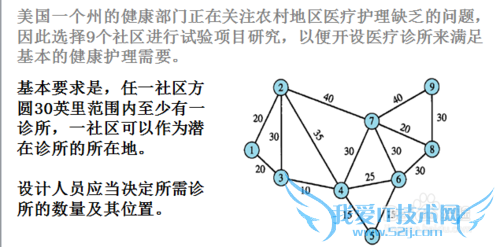

前期准备工作(包括相关工具或所使用的原料等)
Excel 2010详细的操作方法或具体步骤
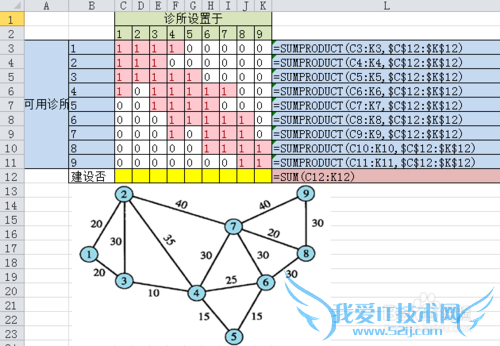
1.设置可达性矩阵
列C到列K表示诊所建设的事
第3行到第11行就是9个社区可用诊所数量的事;
区域【C12:K12】为可变单元格(决策变量)——取值表示建设不建设诊所
于是区域【C3:K11】这个矩阵就是“可达性矩阵”
------------
我们以C列为例,如果社区1建设诊所(C3=1),那么根据地图,我们可以看到
1——>1, 0
1——>2, 20
1——>3, 20
1——>4, 20+10=30
只有这4个社区在30英里范围内,所以只有【C3】、【C4】、【C5】和【C6】的取值为1(可以抵达,可以覆盖),【C5】、【C6】、【C7】、【C8】和【C9】取值为0
------------
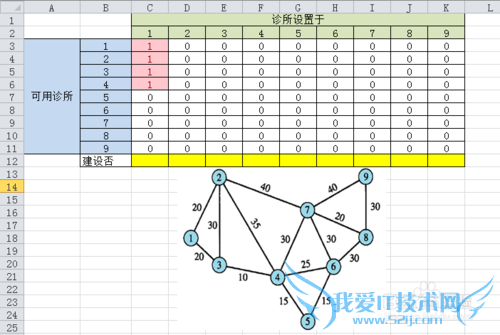
我们可以先设置可达性矩阵(【C3:K11】)为0,然后1列1列的根据地图,把可达的边更改为数值1
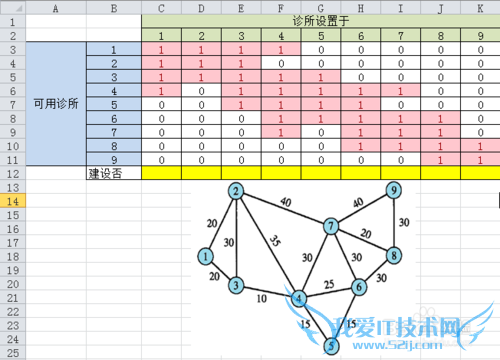
2.目标函数
设置目标函数,在单元格【L12】输入函数【=SUM(C12:K12)】
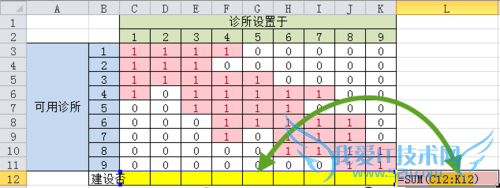
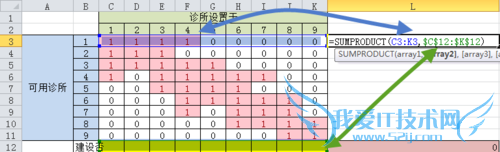
3.每个社区可达的诊所总数
***在单元格【L3】输入函数【=SUMPRODUCT(C3:K3,$C$12:$K$12)】
***选中单元格【L3】,移动鼠标,当鼠标呈黑色小十字时,向下拖拽到单元格【L11】
--------------------
sumproduct函数包括两个单词,sum(求和)、product(乘法),所以意思“先乘,后求和”
本公式中区域【C4:E5】内的单元格与区域【C11:E12】内的单元格分别先乘后求和,只有可覆盖(可达性矩阵取值为1)并且建设诊所(建设否取值为1)才是现实可达的,求和就是总计的可用诊所。
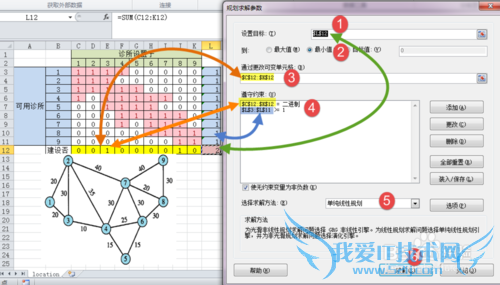
4.规划求解
点击【数据】——【规划求解】
***在弹出的窗口,【设置目标】,点击右侧的按钮,选中单元格【L12】——诊所总数
***其下,点选【最小值】——最少诊所数
***其下,【可变单元格】点击右侧的按钮,选中区域【C12: K12】——9个自变量
***在【规划求解】窗口,点击右侧的【添加】,添加2类约束条件
其一、每个社区可用诊所数>=1
其二、自变量为二分变量
***求解方法,点选【单纯线性规划
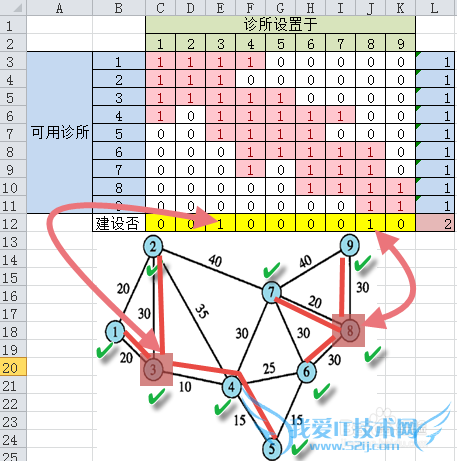
求解结果是,最少建设2个诊所可以,分别位于社区3和社区8
-------------
最优解(2个诊所)是确定的
建设方案可以有不同,获取不同方案的方法就是改变初值。
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
