...若两圆的圆心距等于这个梯形的中位线长，则这两个...

优质解答

∵梯形ABCD的上底是AD、下底是BC，
梯形的中位线长=12

（AD+BC），
∵分别以梯形ABCD的上底AD、下底BC的长为直径作⊙O₁、⊙O₂，
∴⊙O₁、⊙O₂的半径分别为：12

AD，12

BC，
∵12

AD+12

BC=12

（AD+BC），两圆的圆心距等于这个梯形的中位线长，
∴这两个圆的位置关系是外切．
故选B．

其他类似问题

问题1：分别以梯形ABCD的上底AD、下底BC的长为直径作⊙O1、⊙O2，若两圆的圆心距等于这个梯形的中位线长，则这两个圆的位置关系是（　　）A. 外离B. 外切C. 相交D. 内切[数学科目]

∵梯形ABCD的上底是AD、下底是BC，
梯形的中位线长=12

（AD+BC），
∵分别以梯形ABCD的上底AD、下底BC的长为直径作⊙O₁、⊙O₂，
∴⊙O₁、⊙O₂的半径分别为：12

AD，12

BC，
∵12

AD+12

BC=12

（AD+BC），两圆的圆心距等于这个梯形的中位线长，
∴这两个圆的位置关系是外切．
故选B．

问题2：如图，在直角梯形ABCD中，AD∥BC，∠D=90°，以腰AB为直径作圆，已知AB=10，AD=M，BC=M+4，要使圆与折线BCDA有三个公共点（A、B两点除外），则M的取值范围是（　　） A. 0≤M≤3B. 0＜M＜3C. 0＜M≤3D[数学科目]

根据题意，得圆必须和直线CD相交．
设直线CD和圆相切于点E，连接OE，则OE⊥CD，
则OE∥AD∥BC，
又OA=OB，则ED=EC．
根据梯形的中位线定理，得OE=M+M+42

=M+2，
则M+2=5，M=3，
所以直线要和圆相交，则0＜M＜3．
故选B．

问题3：如图，梯形ABCD中，AD∥BC，DC⊥BC，AB=8，BC=5，若以AB为直径的⊙O与DC相切于E，则DC=______．[数学科目]

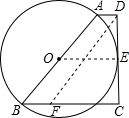连接OE，过D作DF∥AB，梯形ABCD中，AD∥BC，DC⊥BC，AB为直径的⊙O与DC相切于E，故OE⊥CD，OE是梯形ABCD的中位线，OE=12

（BC+AD），即AD=2OE-BC=2×4-5=3．
∵AD∥BC，AB∥DF，
∴四边形ABFD是平行四边形，BF=AD=3，CF=BC-BF=5-3=2，DF=AB=8，CD=

DF

2

?

CF

2

=

8

2

?

2

2

=215

．

问题4：四边形ABCD为直角梯形,垂直于底的腰AB为直径的圆与腰CD相切,AB长8,梯形ABCD的周长28,求上底AD与下底BC.如图,四边形ABCD为直角梯形,以垂直于底的腰AB为直径的圆与腰CD相切,已知AB的长是8cm,梯形ABC[数学科目]

答案：上底为2厘米,下底为8厘米

因为四边形为直角梯形,且AB为直径.取AB边中点E连接CE,DE则角CED为直角 所以有BE*BE+BC*BC=EC*EC (1)AE*AE+AD*AD=DE*DE (2)

因为 DE*DE+EC*EC=CD*CD (3)

所以有（1）（2）式左边的和等于（3）式右边的和 又因为周长为28 AB为8 所以有AD+CD+BC=20 过E做CD的垂线F 有AD=DF BC=FC

所以有CD=10

列方程组：AD+BC=10

(AD*AD+AE*AE)+(BE*BE+BC*BC)=ED*ED+EC*EC=CD*CD=100

解得AD=2 BC=8

问题5：直角梯形ABCD中,AD平行BC,角B等于90度,且AD+BC等于CD,第一问以CD为直径作圆O,求证第二问以CD为直径作圆O,求证CD与圆O一点相切 上面就是一个abco的梯形,没有以谁为圆心[数学科目]

第一问：

设AB中点为E,连接OE,则OE是梯形的中位线,可以得到OE//AD//BC,则OE⊥AB.

又中位线OE=（AD+BC）/2=CD/2

则可知AB垂直于OE,且垂距为半径,由圆的定理可知圆O与AB相切.

第二问：

AB的中点是E,连接DE,CE,作EF⊥CD于F

下面需要证明EF等于半径

设AB=2x

S梯形=1/2（AD+BC）*AB

=1/2CD*2x

S△ADE=AD*x/2,S△BCE=BC*x/2,S△CDE= CD*EF/2

则S总=AD*x/2+BC*x/2+CD*EF/2

=（AD+BC）x/2+CD*EF/2

=CD*x/2+CD*EF/2

由S梯形=S总可得EF=x

综上,E到CD的距离是圆的半径,则CD与圆相切.