阴径增长的方法_...AB长为4cm，且CD⊥AB于O，你能借助旋转的方法求出图...[数学]

精选知识

用割补法明显看出,阴影部分面积=圆面积的1/4

∴S阴=1/4×2×2×π

=π（平方厘米）

其他类似问题

问题1：1.如图,圆O中直径AB与CD互相垂直,AB=10cm,以C为圆心,CA为半径画弧AEB,求月牙形(阴影部分)面积2,如图正方形的边长为32厘米,求图中阴影部分的面积.3,一个直径为4厘米的半圆,让点A不动,把整个半圆[数学科目]

答：

1、因为AB⊥CD根据勾股定理：

AC2=（10÷2）2+（10÷2）2=50

AC=5√2

∠ACB=90°（直径所对的圆周角）

弓形ABE的面积

=S扇形AEBC -SΔABC=∏×(5√2)2×90/360-10×5÷2

=25∏/2-25

s阴=S半圆-S弓形ABE

=25∏/2-(25∏/2-25)

=25cm2

3、首先,扇形ABC的面积为：

πR^2×45/360=2π；

半圆形的面积为：

0.5×πr^2=2π；

所以整个图形的面积是4π；

现用总的面积减去空白部分,也就是半圆的面积,得到的就是阴影部分的面积 2π

第2题没想出,只能帮你到这了,亲.

问题2：如图，⊙O的直径EF为10cm，弦AB、CD分别为6cm、8cm，且AB∥EF∥CD．则图中阴影部分面积之和为______．[数学科目]

如图，作直径MN，使MN⊥EF于O，交AB于G，交CD于H；连接OA、OB、OC、OD；
在Rt△OBG中，BG=3cm，OB=5cm，因此OG=4cm；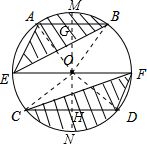
同理：在Rt△OCH中，CH=4cm，OC=5cm，因此OH=3cm；
sin∠DOF=OHOD=35，sin∠BOF=OGOB=45，sin∠COE=OHOC=35，
sin∠AOE=OGOA=45；即∠DOF=∠AOM=∠COE=∠BOM，∠CON=∠DON=∠AOE=∠BOF
因此S_扇形OAE=S_扇形OBF=S_扇形CON=S_扇形ODN；
∴S_阴影=S_△ABE+S_弓形AMB+S_△CDF+S_弓形CND
=S_△OAB+S_弓形AMB+S_△OCD+S_弓形CND
=S_扇形OAB+S_扇形OCN+S_扇形ODN
=S_扇形OAB+S_扇形OAE+S_扇形OBF
=12S_⊙O
=25π2cm²．

问题3：如图三个圆的圆心均为点o,ab是线段长为3cm的线段,cd⊥ab于o,你能借助旋转的知识求出阴影部分面积吗π不取近似值[数学科目]

根据对称性可知,阴影部分其实是四分之一个大圆,面积自然是四分之一大圆的面积!

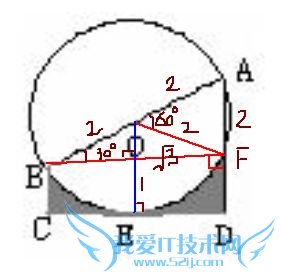
问题4：如图,AB是圆O直径,CD切圆O于E,BC⊥CD,AD⊥CD交圆O于F,∠A=60°,AB=4,求阴影部分面积[数学科目]

刚才看错图形了,现改过来了

设：AD交圆于F,连接OF、BF,因为AB为直径,所以∠BFA=90°

∠OFA=∠A=60°,所以∠AOF=60°,AF=OF=2,∠BOF=120°,

OF=2,所以BF=2√3,O到BF的距离是1,

连接OE,连接OE,则OE⊥CD,O是AB中点,所以OE为梯形ADCB的中位线

OE垂直CD,OE=2,所以弓形BEF的高=2-1=1

阴影面积=梯形ADCB面积-△ABF面积-弓形BEF的面积

=（AD+BC）×BF÷2-BF×AF÷2-（扇形OBF-△OBF）

=4×2√3÷2-√3×2÷2-（π×2²÷3-√3×1÷2）

=4√3-√3-(4/3)π+√3/2

=(7/2)√3--(4/3)π

【2分之7倍根号3-3分之4π】

相信你一定能看明白了

问题5：如图在圆o中直径ab等于2ca切严o与acc交圆o于d若角c等于45度求cd的长二求阴影[数学科目]

图在哪⊙_⊙?