2012年深圳中考数学第16题：已知RT△ABC的直角边AB=5，...

精选知识

以O为圆心OA为半径做个圆,ABCM四个点都在圆上,弦AM所对的圆周角ABM等于45度,再根据余弦定理在三角形ABM中就可以算出 R2=37/2,再根据勾股定理就可以得BC等于7

其他类似问题

问题1：已知RT△ABC的直角边AB=5,以斜边AC为边作正方形ACDE,连接AD、CE 交于M,连接BM,若BM=6√2,则BC=红线的圆可忽略， [数学科目]

∵ACDE是正方形

∴CE⊥AD 即∠AMC=90° ∠ACM=45°

∵∠ABC=90°

∴∠ABC+∠AMC=180°

∴A、B、C、M四点共圆

∴∠ACM=∠ABM=45°

∴根据余弦定理得

AM2=AB2+BM2-2AB×BM×cos45°

=25+72-2×5×6√2×√2/2

=25+72-60

=37

即AM=√37

∵△ACM是等腰直角三角形

∴AC2=2AM2=74

∴BC2=AC2-AB2

=74-25

=49

∴BC=7

问题2：Rt△ABC中,∠B=90°,分别以AB,AC为边,向△ABC外作正方形ACDE和正方形ABGF,连接EF,EC,延长BA交EF于H,求证:Bc=2AH[数学科目]

辅助线：过E作EI∥AF,交AH的延长线于I,连接FI

∠IAE+∠EAC+∠CAB=180o,∠EAC=90o,所以∠IAE+∠CAB=90o

在△ABC中,∠BCA+∠CAB=90o,所以∠IAE=∠BCA

在△ABC和△AEI中,∠IAE=∠BCA,∠AIE=∠ABC=90o,AE=AC,所以△ABC≌△AEI,所以AB=IE,IA=BC

因为AB=FA,所以FA=IE

在四边形FAEI中,IE与FA平行且相等,因此是平行四边形,根据平行四边形性质,IH=AH=1/2*IA,所以BC=2AH,即证.

没有图,自己画个图看看.

问题3：Rt△ABC中,∠B=90°,分别以AB,AC为边,向△ABC外作正方形ACDE和正方形ABGF,连接EF,EC,延长BA交EF于H求证BC=2AH

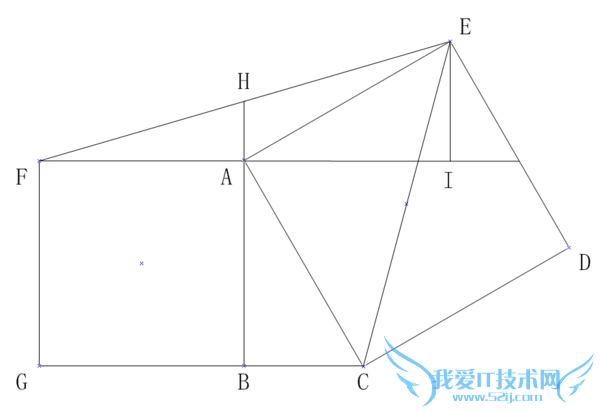
如图,延长FA,过E做FA的垂线,垂足为I

AE = AC

∠EAI = ∠BAC

所以RtΔABC ≌ RtΔAIE

所以

AI = AB , EI = BC

又AF=AB,所以AF=AI

所以AH为ΔFIE的中位线

AH = 1/2 EI

EI=BC

所以AH= 1/2 BC

问题4：以锐角△ABC的边AC,AB为边向外作正方形ACDE和正方形ABGF,连接BE,CF:求BE和CF的关系,说明理由.[数学科目]

在正方形ABGF,

AF=AB,

∠FAB=90°,

又在正方形ACDE,

AE=AC,

∠EAC=90°,

∴∠FAB=∠EAC=90°,

∵∠FAC=∠FAB+∠BAC,

∠EAB=∠EAC+∠BAC,

∴∠FAC=∠EAB,

∴△FAC≌△EAB,

∴BE=CF,且∠AFC=∠ABE,

又∠AOF=∠BOH,

故在△AFO和△BHO中,有∠FAO=∠BHO=90°,

∴BE又垂直于CF；

自己看吧.

问题5：已知RT三角形ABC的斜边AB=1,以AC为边长作正方形ACDE,求SRT△ABC+S正ACDE的最大值[数学科目]

由于Rt△ABC斜边AB=1,故了设直角边AC=sina,BC=cosa,AC²+BC²=sin²a+cos²a=1=AB².

而S△ABC+S□ACDE=0.5AC·BC+AC²=0.5sinacosa+sin²a=0.25sin2a+0.5-0.5cos2a=√(0.25²+0.5²)sin(2a+arctan2)+0.5=(√5)sin(2a+arctan2)/4+0.5,由于正弦函数sinx最大只能为1,所以整个式子的最大值为[(√5)+2]/4.通过sin(2a+arctan2)=1可反解出此时的AC长度.

设AC=b,BC=a,AB=1,勾股定理可解a=√(1-b²),整个图形面积S=0.5ab+b²=0.5b·√(1-b²)+b²=0.5√[b²(1-b²)]+b².可以令x=b²,则原式=0.5√(x-x²)+x=0.5√(-x²+x-1/4+1/4)+x=0.5√[0.25-(x-0.5)²]+x……这个题配方法求最大值有点困难,因为根式中的二次函数不是单调函数,在x＞0.5的时候,根式中的二次函数单调递减,而x是单调递增函数,通过这样的配方法如果不把最后的x配进去,算出的结果无法证明是最大……遇到这样的情况一般是用函数求导,拉格朗日判别式求最值.我觉得这题用初中的办法太难了,高中方法就像⒈那么解,而拉格朗日判别式是大学高等数学的内容.