欢迎您访问52IJ教育培训网,今天小编为你分享的学习资料方面的学习知识是通过网络精心收集整理的:“微分方程_微分方程一曲线过点(2a,b),它以[a,x]为底构成的曲边...”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
一依题意可得
∫ydx(a到x)=y(x-a)/m
两边求导得到my=-ay‘+y+y’x
得到(m-1)y=(x-a)dy/dx 推出(m-1)dx/(x-a)=dy/y
所以(m-1)ln(x-a)=lny+lnc
得到y=(x-a)^(m-1)/c
又曲线经过(2a,b)
所以c=a^(m-1)/b
所以曲线方程是y=b(x/a-1)^(m-1)
其他类似问题
问题1:微分方程y''-3y'+2y=5,y(0)=1,y'(0)=2求解过程[数学科目]
分为齐次解和特解
y''-3y'+2y = 0
特征方程:r^2 - 3r + 2 = 0
r= 1 或 2
y = c1*e^x + c2*e^(2x)
y* = c3
代入原方程得:0-0+2c3=5
c3=5/2
所以原方程的通解是y=c1*e^x + c2*e^(2x)+5/2
y(0)=1,即c1+c2+5/2=1
y'=c1*e^x+2*c2*e^(2x)
y'(0)=2,即c1+2c2=2
解得c1=-5,c2=7/2
所以原方程的解是y=-5*e^x + 7/2 *e^(2x)+5/2
问题2:解微分方程y`=1/(x-y)+1答案(x-y)^2+2x=c[数学科目]
做变量替换
u=x-y,两边对x求导
u'=1-y'
原方程变为u‘=-(1/u)
积分换回原变量得结果(x-y)^2+2x=c
问题3:求微分方程y″-5y′+6y=xe2x的通解.[数学科目]
方程y″-5y′+6y=xe2x的特征方程为:
λ2-5λ+6=0,
特征根为:λ1=2,λ2=3.
因为2是方程的单重特征根,
故方程y″-5y′+6y=xe2x的特解形式为:
y*=x(Ax+B)e2x.
代入方程整理可得,-2Axe2x+(2A-B)e2x=xe2x,
因此,?2A=12A?B=0
故方程的通解为:y=
C
1e
2x+C
2e
3x?x2(x+2)e
x.问题4:简谐运动微分方程的怎样推导?[物理科目]
简谐运动特征及表式:1F=-kx(回复力)
2 d^2x/dt^2=-(k/m)x 取k/m=w^2 所以d^2x/dt^2=-(w^2)x d^2x/dt^2+(w^2)x=0 .
x''=-w^2x
r^2=-1,所以r=+-wi,通解 x=c1coswt+c2sinwt=Ccos(wt+fai),带入振幅A,C=A,得 x=Acos(wt+φ)
问题5:微分方程
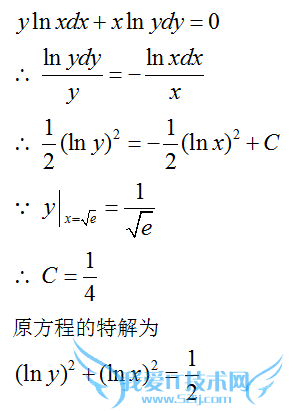
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
