同学们提问关于“80海里_...与灯塔P的距离为80海里的A处经正南方向航行一段时...[数学]”的问题，52IJ师说平台通过网络上精心整理了以下关于“80海里_...与灯塔P的距离为80海里的A处经正南方向航行一段时...[数学]”的一些有用参考答案。请注意：文中所谈及的内容不代表本站的真正观点，也请不要相信各种联系方式。下面是本网所整理的“80海里_...与灯塔P的距离为80海里的A处经正南方向航行一段时...[数学]”的相关信息：
本文发布时间:2016-04-13 10:54 编辑:勤奋者
?
问题
...与灯塔P的距离为80海里的A处经正南方向航行一段时...
科目：数学 关键词：80海里
优质解答
∴PC=PA?cos∠APC=403 （海里）．（2分）
在Rt△PCB中，cos∠BPC=PCPB，（1分）
∴PB＝PCcos∠BPC＝403cos45°＝406（海里）．
答：此时轮船所在的B处与灯塔P的距离是406海里．（2分）
∴PC=PA?cos∠APC=403 （海里）．（2分）
在Rt△PCB中，cos∠BPC=PCPB，（1分）
∴PB＝PCcos∠BPC＝403cos45°＝406（海里）．
答：此时轮船所在的B处与灯塔P的距离是406海里．（2分）
答案是87.457,如果精确到0.01就是87.46.此题方法如下：本题中“正南方向航行”是关键,于是我们可以轻松找到直角,再利用简单的三角函数,连续设两次未知数即可得出答案
其他类似问题
问题1：如图，一艘海轮位于灯塔P的北偏东60°方向上，它沿正南方向航行70海里，到达位于灯塔P的南偏东30°方向的B处，问此时，海轮距离灯塔P多远？[数学科目]
∵一艘海轮位于灯塔P的北偏东60°方向上，到达位于灯塔P的南偏东30°方向的B处，
∴∠APB=90°，
∵PN∥AB，
∴∠B=30°，
∵AB=70，
∴PB=AB?cosB=70×cos30°=353
问题2：如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，求此时轮船所在的B处与灯塔P的距离（结[数学科目]
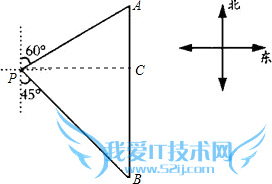作PC⊥AB于C点，
∴∠APC=30°，∠BPC=45° AP=80（海里）．（2分）
在Rt△APC中，cos∠APC=PCPA
∴PC=PA?cos∠APC=403 （海里）．（2分）
在Rt△PCB中，cos∠BPC=PCPB，（1分）
∴PB＝PCcos∠BPC＝403cos45°＝406（海里）．
答：此时轮船所在的B处与灯塔P的距离是406海里．（2分）
问题3：如图，一艘海轮位于灯塔P的北偏东60°方向上，它沿正南方向航行70海里，到达位于灯塔P的南偏东30°方向的B处，问此时，海轮距离灯塔P多远？[数学科目]
∵一艘海轮位于灯塔P的北偏东60°方向上，到达位于灯塔P的南偏东30°方向的B处，
∴∠APB=90°，
∵PN∥AB，
∴∠B=30°，
∵AB=70，
∴PB=AB?cosB=70×cos30°=353
问题4：如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，求此时轮船所在的B处与灯塔P的距离（结[数学科目]
作PC⊥AB于C点，
∴∠APC=30°，∠BPC=45° AP=80（海里）．（2分）
在Rt△APC中，cos∠APC=PCPA
∴PC=PA?cos∠APC=403 （海里）．（2分）
在Rt△PCB中，cos∠BPC=PCPB，（1分）
∴PB＝PCcos∠BPC＝403cos45°＝406（海里）．
答：此时轮船所在的B处与灯塔P的距离是406海里．（2分）
问题5：一艘轮船位于灯塔p的北偏东60°方向上的A处,它沿正南方向航行80海里后,到达位于灯塔P的南偏东45°方向上B处,这时,海轮所在B处距离灯塔P有多远[数学科目]
根据题意,知：∠PAB=60°,∠APB=45°+30°=75°,AB=80海里,所以BP=AB*sin∠PAB/sin∠APB=80*sin60°/sin75°=120√2-40√6.
- 评论列表（网友评论仅供网友表达个人看法，并不表明本站同意其观点或证实其描述）
-