同学们提问关于“b2区间_已知关于x的一元二次方程x2-2ax+b2=0.(1)若a是从0、1...[数学]”的问题，52IJ师说平台通过网络上精心整理了以下关于“b2区间_已知关于x的一元二次方程x2-2ax+b2=0.(1)若a是从0、1...[数学]”的一些有用参考答案。请注意：文中所谈及的内容不代表本站的真正观点，也请不要相信各种联系方式。下面是本网所整理的“b2区间_已知关于x的一元二次方程x2-2ax+b2=0.(1)若a是从0、1...[数学]”的相关信息：
本文发布时间:2016-04-13 14:53 编辑:勤奋者
?
问题
已知关于x的一元二次方程x2-2ax+b2=0.(1)若a是从0、1...
科目：数学 关键词：b2区间
优质解答
答：方程x2-2ax+b2=0没有实根的概率为14．-------（7分）
（2）设事件B为“方程x2-2ax+b2=0无实根”；----（8分）
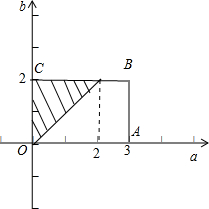
如图，试验的所有基本事件所构成的区域为矩形OABC：{（a，b）|0≤a≤3，0≤b≤2}，
其中构成事件B的区域为三角形OEC，即{（a，b）|0≤a≤3，0≤b≤2，a＜b}，
由于点（a，b）落在区域内的每一点是随机的，----------（10分）
∴事件B发生的概率P（B）=
答：方程x2-2ax+b2=0没有实根的概率为13．--------（14分）
（1）设事件A为“方程x2-2ax+b2=0无实根”；--------（1分）
当△=4a2-4b2=4（a2-b2）＜0，即a＜b时，方程x2-2ax+b2=0无实根．---------（3分）
所有的（a，b）共12个：（0，0），（0，1），（0，2），（1，0），（1，1），（1，2），
（2，0），（2，1），（2，2），（3，0），（3，1），（3，2）．
其中，第一个数表示a的取值，第二个数表示b的取值．
事件A包含3个基本事件（0，1），（0，2），（1，2），
由于每个基本事件发生的可能性都相同，------（4分）
∴事件A发生的概率P（A）=312
答：方程x2-2ax+b2=0没有实根的概率为14．-------（7分）
（2）设事件B为“方程x2-2ax+b2=0无实根”；----（8分）
如图，试验的所有基本事件所构成的区域为矩形OABC：{（a，b）|0≤a≤3，0≤b≤2}，
其中构成事件B的区域为三角形OEC，即{（a，b）|0≤a≤3，0≤b≤2，a＜b}，
由于点（a，b）落在区域内的每一点是随机的，----------（10分）
∴事件B发生的概率P（B）=
S
△OECS
OABC=12×2×23×2=13．-------（13分）答：方程x2-2ax+b2=0没有实根的概率为13．--------（14分）
- 评论列表（网友评论仅供网友表达个人看法，并不表明本站同意其观点或证实其描述）
-