CF是三角形ABC的AB边上的高，FP垂直BC，FQ垂直AC，求证A...

优质解答

证明：

连接PQ

∵AF⊥BC,FP⊥BC,FQ⊥AC

∴:∠CFP+∠PFB=:∠B+∠PFB=90°,

∴:∠CFP=∠B

又∠FPC+∠FQC=180°,

∴:F,P,C,Q四点共圆

∴:∠CQP=∠CFP（同弧所对应的圆周角相等）

∴:∠CQP=∠B

∵:∠CQP+∠PQA=180°,

∴:∠B+∠PQA=180°,

∴:,A,B,P,Q四点共圆

其他回答

CP/CF=sin50° CQ/CF=sin60° CP/CQ=sin50°/sin60° sin50°/sin∴△ACB∽△PCQ ∠CQP=50° 方法3: CQFP四点共圆∠CQP=50°

其他类似问题

问题1：在三角形ABC中,∠A=60°,∠C=70°,CF⊥AB,FQ⊥AC,FP⊥BC,求∠CQP[数学科目]

50度,因为FQ⊥AC,FP⊥BC,所以P,Q,F四点共圆,所以角CQP=角CFP,有条件知角CFP为50度

问题2：CF是△ABC的AB边上的高,FP⊥BC,FQ⊥AC,求证：A、B、P、Q四点共圆

FP⊥BC,FQ⊥AC

所以CPFQ四点共圆

所以∠QCF=∠QPC

∠QCF+∠QFA=90

∠A+∠QFA=90

所以∠A=∠QCF=∠QPC

因为∠QPC+∠QPB=180

所以∠A+∠QPB=180

所以A、B、P、Q四点共圆

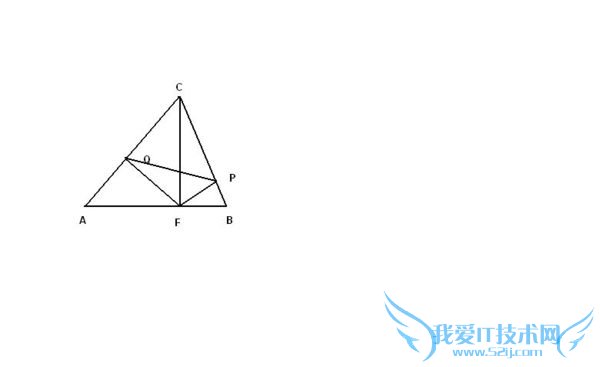
问题3：（《几何证明选讲》选做题）如图，在△ABC中，∠A=60°，∠ACB=70°，CF是△ABC的边AB上的高，FP⊥BC于点P，FQ⊥AC于点Q，则∠CQP的大小为______．[数学科目]

由FP⊥BC，FQ⊥AC，得C、Q、F、P四点共圆，所以∠CQP=∠CFP=∠B=180°-（∠A+∠C）=180°-（60°+70°）=50°．
故答案为：50°．

问题4：三角形ABC分别AB,AC为边作正方形ABGE和ACHF直线AD垂直BC于点D,EF垂直AD于点P,FQ垂直AD于点Q说明EP=FQ急求!

本题题目中“EF垂直AD于点P”好像有误,应为“EP垂直AD于点P”,

如果“EP垂直AD于点P”可以证明：

正方形边长相等,所以AB=AE,（边）

在三角形ABD中,角ABD与角BAD互为余角

而角BAD与角EAP互为余角,所以

角ABD=角EAP,（角）

同理,角BAD=角PEA,（角）

那么三角形ABD=三角形EAP（角边角）,

那么EP=AD

同理可证FQ=AD

因此EP=FQ

证毕

问题5：如图,等边三角形ABC中,AB=1,P是AB上的一个动点,作PE垂直BC,EF垂直AC,FQ垂直AB,垂足分别为E,F,Q.（1）设BP=x,AQ=y,求y与x之间的函数解析式 （2）当点P和点Q重合时,求线段EF的长 （3）当点P和点Q不重合

我是一个叫玫瑰的女孩子,前几年爱上了一个叫高的男孩,我不知道他是否爱我,但是我很爱他,我不敢向他表达爱意,他的姐姐是一个很阴险毒辣的女孩,她也爱高,当她知道我爱高,高也爱我时,她很气愤,她把我的高杀了,我最后因为情绪失控而自杀了,到天上陪伴我的高,这个女孩子叫宁.这是一个恶毒的咒语,请你在收到的一个小时中转发五个论坛,否则你将会失去最爱的人,最后全家因为你而死,如果你发的话,你在十天之内你爱的人也会爱你.我也是迫不得已,因为我不想失去最爱的人,对不起