设变量x，y满足约束条件2x？y？2≤0x？2y+2≥0x...

精选知识

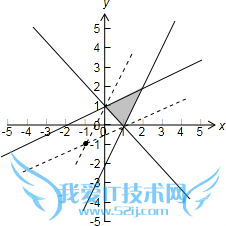满足约束条件2x?y?2≤0x?2y+2≥0x+y?1≥0

的可行域如下图所示：
根据题意，s=y+1x+1

可以看作是可行域中的一点与点（-1，-1）连线的斜率，
由图分析易得：当x=1，y=O时，其斜率最小，即s=y+1x+1

取最小值12

当x=0，y=1时，其斜率最大，即s=y+1x+1

取最大值2
故s=y+1x+1

的取值范围是[12

，2]
故选D

其他类似问题

问题1：若变量x，y满足约束条件3≤2x+y≤96≤x?y≤9，则z=x+2y的最小值为______．[数学科目]

由约束条件3≤2x+y≤96≤x?y≤9

作出可行域如图，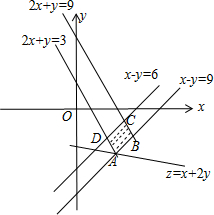

化目标函数z=x+2y为直线方程的斜截式y＝?12x+z2

，
由图可知，当直线过A点时直线在y轴上的截距最小，
联立2x+y＝3x?y＝9

，解得A（4，-5）．
∴z=4+2×（-5）=-6．
故答案为：-6．

问题2：设变量x，y满足约束条件x≥0x?y≥02x?y?2≤0则z=3x-2y的最大值为______．[数学科目]

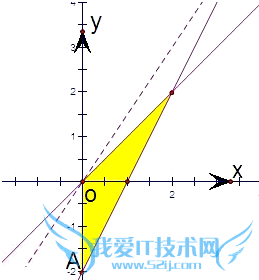依题意，画出可行域（如图示），
则对于目标函数z=3x-2y，
当直线经过A（0，-2）时，
z取到最大值，Zmax=4．
故答案为：4．

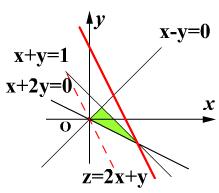
问题3：设变量x,y满足约束条件 {x-y≥0,x+y≤1,x+2y≥0},则函数Z=2x+y 的最大值?[数学科目]

可行域是由三条直线x-y=0,x+y=1,x+2y=0围成的三角形,目标函数z=2x+y中的z表示直线y=-2x+z的截距,当目标函数z=2x+y经过直线x+y=1,x+2y=0的交点（2,-1）时,z有最大值为

z=2×2-1=3

问题4：设变量x，y满足约束条件x+2y?5≤0x?y?2≤0x≥0，则目标函数z=2x+3y+1的最大值为______．[数学科目]

作出不等式组x+2y?5≤0x?y?2≤0x≥0

表示的平面区域，
得到如图的△ABC及其内部，其中A（3，1），B（0，-2），C（0，2）

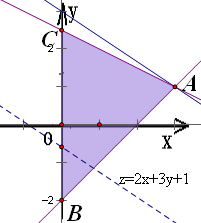
设z=F（x，y）=2x+3y+1，将直线l：z=2x+3y+1进行平移，
当l经过点A（3，1）时，目标函数z达到最大值
∴z_最大值=F（3，1）=10
故答案为：10

问题5：设变量满足约束条件x+y≥3,x-y≥-1,2x-y≤3,则目标函数z=2x+2y最小值?

1.可以用初中的图解法来做,画个坐标轴,根据条件得到可行域,然后平移目标函数得到最小值.

2.可以用excel中的规划求解宏来做

3.可以用lingo编程来做

4.也可以用matlab,但不建议.

其实这道题不难,就用第一种方法就能很快求出来,最后的结果是（1.5,1.5）,z=6.这只是其中的一个解,最后的答案是有无数个解,比如（2,1）（1,2）等都是最优解,对应的z的最小值都为6.

另外：再解释一下为什么会有无数个最优解,这是因为目标函数的斜率和其中一个约束条件x+y≥3的斜率相等的缘故.