如图直角梯形abcd中_在直角梯形ABCD中，∠C=90°，高CD=6cm，底BC=10cm(如图...[数学]

精选知识

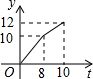
（1）设：设M，N所在直线的解析式为y=tx+b，把点M与N的坐标（4，5）和(2，52)

，分别代入得：5＝4t+b52＝2t+b

，
解得：t=54

，b=0．
∴M，N所在直线的解析式为y=54

x；
（2）∵P在AB段与AD段的解析式不同，
∴AB段：y=tcosB

，
∴AD段：y=6sinA

（此处为AB段长度）+t-6tanB

（此处为Q运动到A点时，BQ的长度），由（1）可知，cosB=45

，
又∵CD=6cm，BC=10cm
∴由勾股定理可得AB=10CM，AD=2CM．
（3）由（2）可知：AB段：y=54

t（t＜8）；
AD 段：y=t+2 （8≤t≤10），再画函数的图象即可．

其他类似问题

问题1：在直角梯形ABCD中，∠C=90°，高CD=6cm，底BC=10cm（如图1）．动点Q从点B出发，沿BC运动到点C停止，运动的速度都是1cm/s．同时，动点P也从B点出发，沿BA→AD运动到点D停止，且PQ始终垂直BC．设P，[数学科目]

（1）设：设M，N所在直线的解析式为y=tx+b，把点M与N的坐标（4，5）和(2，52)

，分别代入得：5＝4t+b52＝2t+b

，
解得：t=54

，b=0．
∴M，N所在直线的解析式为y=54

x；
（2）∵P在AB段与AD段的解析式不同，
∴AB段：y=tcosB

，
∴AD段：y=6sinA

（此处为AB段长度）+t-6tanB

（此处为Q运动到A点时，BQ的长度），由（1）可知，cosB=45

，
又∵CD=6cm，BC=10cm
∴由勾股定理可得AB=10CM，AD=2CM．
（3）由（2）可知：AB段：y=54

t（t＜8）；
AD 段：y=t+2 （8≤t≤10），再画函数的图象即可．

问题2：在直角梯形ABCD中,∠C=90°,高CD=6cm,底BC=10cm（如图1）． 动点Q从点B出发,沿BC运动到点C停止运动的速度都是1cm/s．同时,动点P也从B点出发,沿BA→AD运动到点D停止,且PQ始终垂直BC．设P,Q同时从点B出[数学科目]

1,mn直线解析式：y=5t/4

2,显然P在AB段与AD段的解析式不同,AB段：y=t/cos∠b,AD段:y=6/sin∠B(此处为AB段长度)+t-6/tan∠B（此处为Q运动到A点时,BQ的长度）,由第一问可知,显然y=5t/4为AB段的解析式,即cos∠b=4/5,由勾股定理可推出AB段=10CM,AD段=2CM,

3.由第二问可知：AB段:y=5t/4 t

问题3：如图，在直角梯形ABCD中，∠B=90°，AD∥BC，且AD=4cm，AB=6cm，DC=10cm．若动点P从A点出发，以每秒4cm的速度沿线段AD、DC向C点运动；动点Q从C点出发以每秒5cm的速度沿CB向B点运动．当Q点到达B点时[数学科目]

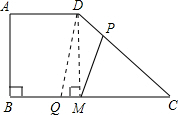（1）作DM⊥BC于点M．则四边形ABMD是平行四边形
∴DM=AB=6cm．
在直角△CDM中，CM=

CD

2

?

DM

2

=8cm
∴BC=BM+CM=4+8=12cm
∴直角梯形ABCD的面积为12

（AD+BC）?AB=48cm²；
（2）当PD=CQ时，四边形PQCD成为平行四边形
即4-4t=5t
解得t=49

；
（3）BQ=12-5t
在直角△ABQ中，AB²+BQ²=AQ²
即6²+（12-5t）²=10²
解得t=45

；
（4）存在，t＝74

．
连接QD，则CP=14-4t，CQ=5t
若QP⊥CD，则2S_△DQC=CQ×AB=CD×QP
得QP=3t
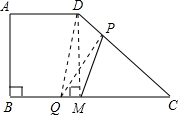
在Rt△QPC中
QP²+PC²=CQ²，即（3t）²+（14-4t）²=（5t）²
解之得t＝74

求得BC=12
CP=14-4t=7＜10
CQ=5t=354

＜12
所以，存在t，使得P点在线段DC上，且PQ⊥DC．

问题4：在直角梯形ABCD中,∠C=90o,高CD=6cm(如图1).动点P,Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到C点停止.两点运动时的速度都是lcm/s.而当点P到达点A时,点Q正好到达点C.设P,Q同时从点B出发[数学科目]

（1）设动点除法t秒后,点P到达点A且点Q正好到达点C时,BC=BA=t,

则S△BPQ=1/2 * t *6=30,∴t=10（秒）

则BA=10cm,AD=2cm

（2）可得坐标为M（10,30）,N（12,30）

（3）当点P在BA上时,y=1/2 * t * sinB =3t²/10 （0≤t＜10）

当点P在DC上时,y=1/2 * 10 * （18-t）=-5t+90 (12＜t≤18)

问题5：如图，在直角梯形ABCD中，∠B=90°，AD∥BC，且AD=4cm，AB=6cm，DC=10cm．若动点P从A点出发，以每秒4cm的速度沿线段AD、DC向C点运动；动点Q从C点出发以每秒5cm的速度沿CB向B点运动．当Q点到达B点时[数学科目]

（1）作DM⊥BC于点M．则四边形ABMD是平行四边形
∴DM=AB=6cm．
在直角△CDM中，CM=

CD

2

?

DM

2

=8cm
∴BC=BM+CM=4+8=12cm
∴直角梯形ABCD的面积为12

（AD+BC）?AB=48cm²；
（2）当PD=CQ时，四边形PQCD成为平行四边形
即4-4t=5t
解得t=49

；
（3）BQ=12-5t
在直角△ABQ中，AB²+BQ²=AQ²
即6²+（12-5t）²=10²
解得t=45

；
（4）存在，t＝74

．
连接QD，则CP=14-4t，CQ=5t
若QP⊥CD，则2S_△DQC=CQ×AB=CD×QP
得QP=3t
在Rt△QPC中
QP²+PC²=CQ²，即（3t）²+（14-4t）²=（5t）²
解之得t＝74

求得BC=12
CP=14-4t=7＜10
CQ=5t=354

＜12
所以，存在t，使得P点在线段DC上，且PQ⊥DC．