弗曼_以数据集{4，5，6，7，10，12，18}为结点权值，画出构造的哈弗曼树.[数学]

精选知识

问题一：

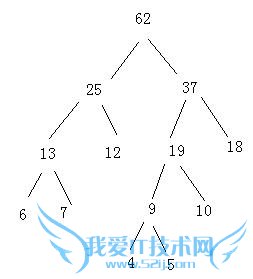
带权路径长度：6×3+7×3+12×2+4×4+5×4+10×3+18×2=18+21+24+16+20+30+36=165

问题二：

深度6

先序：EBADCFHGIKJ

中序：ABCDEFGHIJK

后序：ACDBGJKIHFE

形态：

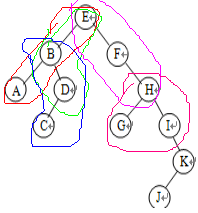
其他类似问题

问题1：给出以数据序列{10,2,7,13,9,12,18}为节点权植所构造的哈弗曼树并计算该树的加权路径和长度WPL.[数学科目]

1:那么首先取出最小的两个,即2,7.构成以下图案.

9

| |

2 7

集合便成为了 {7,9,10,12,13,18}

2：从中选出两个最小的.即 7 ,9.

即变成 16

| |

9 7

| |

2 7

集合即变成了{10,12,13,16,18}

3:从中选取两个最小的.即 10,12；

即构成：

22

| |

10 12

集合即变成了{13,16,18,22}

4：从中选取两个最小的.即13,16.

即变成 29

| |

16 13

| |

9 7

| |

2 7

集合变成了{18,22,29}；

5：同样,取出18,22；

即构成：

40

| |

22 18

| |

10 12

集合即变成{29,40}；

6：将29,40,联合起来.

69

| |

29 40

| | | |

16 13 22 18

| | | |

9 7 10 12

| |

2 7

即变成了{69}；

那么就已经完成了.

可以看到最初的集合里的数都变成了叶子.

WPL就是用 叶子节点乘以它的层数,然后 累加起来就是啦.

即（13+18）*2+（7+10+12）*3+（2+7）*4 =205.

注意：是用 【叶子节点】 乘以 层数.根为第0层.

参考下我回答过的 参考资料,

问题2：数据结构与算法：以数据集{4,5,6,7,10,12,18}为结点权值所构造的哈夫曼树,其带权路径长度为?[数学科目]

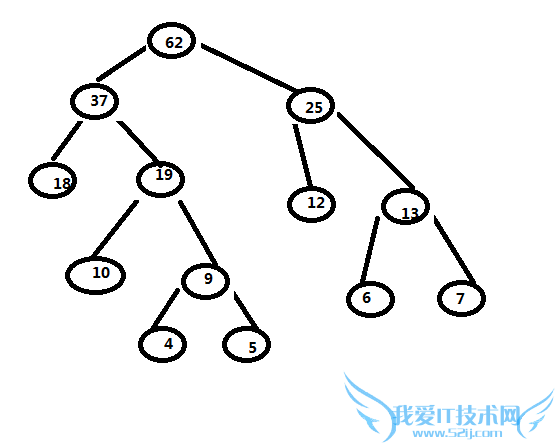
带全路径长度：（4+5）*4+（6+7）*3+10*3+12*2+18*2=165

问题3：有6个节点,权值分别为2,3,4,6,7,15,构成哈弗曼树,求带全路径长度?最好画出构造的哈弗曼树.[数学科目]

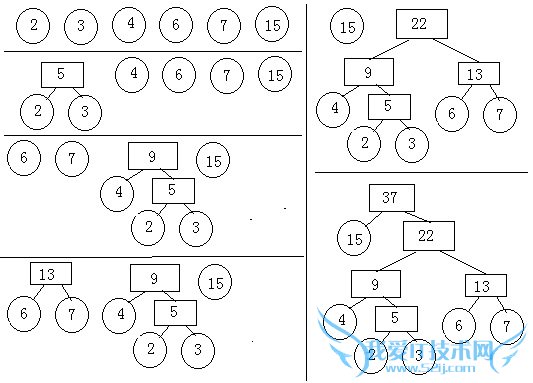
WPL=15+3(4+6+7)+4(2+3)=15+51+20=86

问题4：构造哈夫曼树：以数据集（3,4,5,8,11,18,20,30）为结点,构造一棵哈夫曼数,并求其带权路径长度.[数学科目]

构建哈夫曼树的步骤：

1,选取结点（node）中最小的两个,相加,构成一个新结点

2,重复第一步,直至所有结点都在同一个树型里面.

所以,大概构成后就是这样

.81

.0/ \1

./ \

.31 50

.0/ \1 0/\1

./ \ / \

.18 13 20 30

.0/ \1 0/ \1

./ \ / \

.7 11 5 8

.0/ \1

./ \

.3 4

从最下面向上读,node3和node4是初始数据里面最小的两个,

它们组成一个新结点7,

然后再重复相同的步骤,在新数据里面,7和11是最小,他们组成18,

原始数据里面的18可以消去.

重复步骤直至所有结点在同一个树型里面

现在看看

3的哈夫曼编码就是0000,而数字最大的30编码就是11

问题5：构造哈弗曼树~8,2,5,3,2,17,4 并求 WPL~我算的是103可我同学算的100~[数学科目]

是100

（2+2）*5+3*4+（4+5+8）*3+17=100