欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“射击标靶_某人向一个半径为6的圆形标靶射击,假设他每次射击必...[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
6 2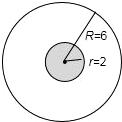 整个靶子是下图中所示的大圆,
整个靶子是下图中所示的大圆,
而距离靶心距离小于2用下图中阴影部分的小圆所示:
故此人射击中靶点与靶心的距离小于2的概率P=π π
| 1 |
| 9 |
故选B.
其他类似问题
问题1:某运动员在场地A和场地B各射击2次,其中在场地A射中靶的概率为1/2,在场地B射中靶的概率为p(0[数学科目]
Xa表示A场地射中次数,Xa=0、1、2的概率分别为1/4,1/2,1/4
Xb表示B场地射中次数,Xb=0、1、2的概率分别为(1-p)的平方,2(1-p)p,p的平方
(1)1/2=p2,所以p=1/4
(2)P{X=O}=P{Xa=0,Xb=0}=P{Xa=0}P{Xb=0}=1/4*(1-p)2(注:2表示平方)
P{X=1}=P{Xa=1,Xb=0}+P{Xa=0,Xb=1}=1/2*(1-p)2+1/4*2(1-p)p=1/2*(1-p)2+1/2(1-p)p
P{X=2}=P{Xa=2,Xb=0}+P{Xa=1,Xb=1}+P{Xa=0,Xb=2}=1/4*(1-p)2+(1-p)p+1/4p2
P{X=3}=P{Xa=1,Xb=2}+P{Xa=2,Xb=1}=1/2*p2+1/4*2(1-p)p=1/2*p2+1/2(1-p)p
P{X=4}=P{Xa=2,Xb=2}=1/4*p2
EX=1+2p(注:次数*对应的概率,然后相加)
(3) P{X=2}=1/4*(1-p)2+(1-p)p+1/4p2=1/4(-2p2+2p+1)=-1/2[(p-1/2)2-3/4]的概率最大,则p=1/2,最大概率为3/8.
终于打完了!解题比打公式简单啊!注意平方的地方哈!
问题2:箭靶直径为1m其中靶心的直径只有12cm,任意向靶射箭射中靶心的概率为多少[数学科目]
概率P=(π*6^2)/(π*50^2)=9/625
问题3:概率论问题:若每次射击击中靶的概率为0.75,射击6次,最有可能命中几次?为什么?[数学科目]
若设X为中靶的次数,则X服从二项分布B(3/4,6)
通过计算可知
P{X=0}= 1/4098
P{X=1}= 18/4096
P{X=2}= 135/4096
P{X=3}= 540/4096
P{X=4}= 1215/4096
P{X=5}= 1458/4096
P{X=6}= 729/4096
显然P{X=5}的概率最大.
我们知道,在一次试验中概率最大那个事件最有可能发生,所以最有可能命中5枪.
没有问题的话就采纳吧.
问题4:一位新兵进行射击训练,共领取了4发子弹,每次击中靶的概率为2/3 1.若射击四次,求恰好两次击中靶的概率2.若规定:当连续两次未击中,则停止射击,否则就打完4发子弹.射击次数为m,求m的分布列
好像是两道题.
1.p=C²4(就是四个里面选两个,实难打出了)×(2/3)²×(1/3)²=8/27
2.这个主要要分析什么时候停止
m 2 3 4
P p1 p2 p3
前两次没打中p1=1/3*1/3=1/9
第一枪中,然后两枪没中p2=2/3*1/3*1/3=2/27
P3计算过程十分复杂,但也简单,因为p3=1-p1-p2
数学期望就把m乘以对应的概率P,不写了,概率还是要画画图,高中老师教的.
问题5:某人射击中靶的概率为p,则在第二次中靶之前已经失败三次的概率

- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
