欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“2010重庆高考数学_2011重庆高考数学试题高为的四棱锥S-ABCD的底面是边...[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
高是四分之根号2 吗?如果是的话
由题意可知:ABCD所在的圆是小圆,对角线长为根号2,四棱锥的高位 四分之根号2,
点S,A,B,C,D均在半径为1的同一球面上,球心到小圆圆心的距离为二分之根号2,定点S在球心距的垂
直平分的平面上,而顶点S到球心的距离为1,所以地面ABCD的中心与顶点S的距离为1.
其他类似问题
问题1:求解一道高考数学选择题: 高为√2/4的四棱锥S-ABCD的底面是边长为1的正方形,点S,A,B,C,D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为A√2/4 B √2/2 C 1 D √2麻烦[数学科目]
令AC与BD的交点为E,过S作平面K∥面ABCD,再过E作EF⊥平面K交平面K于F.
由平行平面间处处等距离,可知:EF=S到面ABCD的距离=√2/4.
令S-ABCD的外接球球心为O.
一、证明:点O在EF的延长线上.
1、点O显然不与F重合.
若重合,则由勾股定理,有:FA^2=EF^2+EA^2.
而FA=1,容易算出:EA=AC/2=√2AB/2=√2/2,得:EF=√[1-(√2/2)^2]=√2/2.
这与EF=√2/4矛盾.
2、点O若在FE的延长线上,则由勾股定理,有:OA^2=OE^2+EA^2.
而OA=1,EA=√2/2,∴OE=√[1-(√2/2)^2]=√2/2.
∴OE+EF=√2/2+√2/4=3√2/4>1,即OF>1,这说明点F在球O外面,自然是不合理的.
由上述的1、2,得:点O在EF的延长线上.
二、证明:F是OE的中点.
由勾股定理,有:OA^2=OE^2+EA^2.
而OA=1,EA=√2/2,∴OE=√[1-(√2/2)^2]=√2/2,又EF=√2/4.
∴点F是OE的中点.
三、计算S到ABCD中心的距离.
连结SF.
∵EF⊥平面K,∴SF⊥EF,又OF=EF,∴S在OE的垂直平分线上,∴SE=SO=1.
∵ABCD是正方形,且E是AC与BD的交点,∴E是ABCD的中心,
∴S到ABCD中心的距离为1.
问题2:(2010重庆市潼南县)如上图,四边形ABCD是边长为1 的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B,D(F),H在同一条直线上,将正方形ABCD沿F→H方向平移至点B与点H重合时停止,设点D、F之[数学科目]
(2010重庆市潼南县)如上图,四边形ABCD是边长为1 的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B,D(F),H在同一条直线上,将正方形ABCD沿F→H
方向平移至点B与点H重合时停止,设点D、F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与 x之间函数关系的图象是(B).
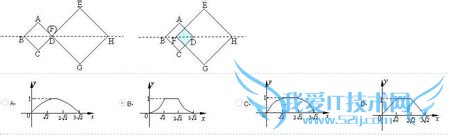
选B.
设DF之间的距离为x.
当0<x<√ 2时,
DF为重叠部分正方形的对角线长.
所以该对角线的边长y为:
z^2+z^2=x^2
z=√ 2/2x.
所以阴影部分面积为:y=z^2=1/2x^2
只看0<x<√ 2部分的图像,即可判断出选B.
问题3:已知|abcd|分之abcd=1,求(abcd分之|abcd|)2011(乘方)+a分之|a|+b分之|b|+c分之|c|+d分之|d|的值[数学科目]
∵|abcd|分之abcd=1
∴abcd为正数
∴a、b、c、d中必定会是四个正数或四个负数或两个正数两个负数
(1)若都是正数
原式=1^2011+1+1+1+1=5
(2)若都是负数,
原式=1^2011-1-1-1-1=-3
(3)若两个正数两个负数,不妨设a<0.b<0
原式=1^2011-1-1+1+1=1
问题4:abcd为整数,abcd相乘积25,abcd相加等于多少?[数学科目]
四个10一下的数每一位相乘等于25,那么将25分解质因数,则25=5×5 那么四个数必定是25=1×1×5×5,那么a、b、c、d中有2个是1,有两个是5,那么相加就是1+1+5+5=12.
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
