欢迎您访问52IJ教育培训网,今天小编为你分享的52ij作业方面的学习知识是通过网络精心收集整理的:“ob_...并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>O...”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
本文发布时间:2016-05-08 22:24 编辑:勤奋者
精选知识
OB EC =OD ED ,即5 4 =OD 6?OD ,
解得OD=10 3 ,
∴S△ABD=1 2 AD?BO=65 3 ,
∴S△POD=65 3 ,
故可得在△POD中,OD边上的高为13,即点P到x轴的距离为13,
∵⊙上的点到x轴的最大距离为9,
∴点P不在⊙上,
故在⊙上不存在点P,使S△ABD=S△POD.
(1)连接AB,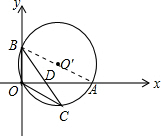
∵∠BOA=90°,
∴AB为直径,由根与系数关系得OA+OB=-k,OA?OB=60,
根据勾股定理,得OA2+OB2=169,
即(OA+OB)2-2OA?OB=169,
解得k2=289,
故k=±17(正值舍去).
则有方程x2-17x+60=0,
解得:x=12或5.
又∵OA>OB,
∴OA=12,OB=5.
(2)若OC2=CD?CB,则△OCB∽△DCO,
∴∠COD=∠CBO,
又∵∠COD=∠CBA,
∴∠CBO=∠CBA,
∴点C是弧OA的中点.
连接O′C交OA于点E,根据垂径定理的推论,得O′C⊥OA,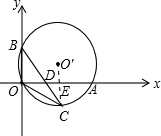
根据垂径定理,得OE=6,根据勾股定理,得O′E=2.5,
故CE=4,即点C坐标为(6,-4).
(3)假定在⊙上存在点P,使S△ABD=S△POD,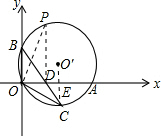
∵OB∥EC,
∴△OBD∽△ECD,
∴
解得OD=
∴S△ABD=
∴S△POD=
故可得在△POD中,OD边上的高为13,即点P到x轴的距离为13,
∵⊙上的点到x轴的最大距离为9,
∴点P不在⊙上,
故在⊙上不存在点P,使S△ABD=S△POD.
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
