本人将带领你,好好了解堆排法。然你不再感到害怕与胆怯(如果有,因为本人原来就是这个样子的)。
前期准备工作(包括相关工具或所使用的原料等)你聪明的大脑你的小手 笔,纸时间 详细的操作方法或具体步骤
堆排序算法介绍
堆是一种重要的数据结构,为一棵完全二叉树, 底层如果用数组存储数据的话,假设某个元素为序号为i(Java数组从0开始,i为0到n-1), 如果它有左子树,那么左子树的位置是2i+1,如果有右子树,右子树的位置是2i+2,如果有父节点,父节点的位置是(n-1)/2取整。分为最大堆和最小堆,最大堆的任意子树根节点不小于任意子结点,最小堆的根节点不大于任意子结点。所谓堆排序就是利用堆这种数据结构来对数组排序,我们使用的是最大堆。处理的思想和冒泡排序,选择排序非常的类似,一层层封顶,只是最大元素的选取使用了最大堆。最大堆的最大元素一定在第0位置,构建好堆之后,交换0位置元素与顶即可。堆排序为原位排序(空间小), 且最好与最坏运行时间是都是O(nlogn)。而且堆排序还是原地算法(in-place algorithm),是渐进最优的比较排序算法。
两个工具类,一个打印一个交换元素
public class ArrayUtils {
public static void printArray(int[] array) {
System.out.print("{");
for (int i=0; i < array.length; i++) {
System.out.print(array[i]);
if (i < array.length - 1) {
System.out.print(", ");
}
}
System.out.println("}");
}
public static void exchangeElements(int[] array, int index1, int index2) {
int temp=array[index1];
array[index1]=array[index2];
array[index2]=temp;
}
}
堆排序的大概步骤如下:
构建最大堆。
选择顶,并与第0位置元素交换
由于步骤2的的交换可能破环了最大堆的性质,第0不再是最大元素,需要调用maxHeap调整堆(沉降法),如果需要重复步骤2
堆排序中最重要的算法就是maxHeap,该函数假设一个元素的两个子节点都满足最大堆的性质(左右子树都是最大堆),只有跟元素可能违反最大堆性质,那么把该元素以及左右子节点的最大元素找出来,如果该元素已经最大,那么整棵树都是最大堆,程序退出,否则交换跟元素与最大元素的位置,继续调用maxHeap原最大元素所在的子树。该算法是分治法的典型应用。具体代码如下:
public class HeapSort {
public static void main(String[] args) {
int[] array={ 3,1,5,6,9,10};
System.out.println("Before heap:");
ArrayUtils.printArray(array);
heapSort(array);
System.out.println("After heap sort:");
ArrayUtils.printArray(array);
}
public static void heapSort(int[] array) {
if (array==null || array.length <=1) {
return;
}
buildMaxHeap(array);
for (int i=array.length - 1; i >=1; i--) {
ArrayUtils.exchangeElements(array, 0, i);
maxHeap(array, i, 0);
}
}
private static void buildMaxHeap(int[] array) {
if (array==null || array.length <=1) {
return;
}
int half=(array.length-1) / 2;
for (int i=half; i >=0; i--) {
maxHeap(array, array.length, i);
}
}
private static void maxHeap(int[] array, int heapSize, int index) {
int left=index * 2 + 1;
int right=index * 2 + 2;
int largest=index;
if (left < heapSize && array[left] > array[index]) {
largest=left;
}
if (right < heapSize && array[right] > array[largest]) {
largest=right;
}
if (index !=largest) {
ArrayUtils.exchangeElements(array, index, largest);
maxHeap(array, heapSize, largest);
}
}
}
手绘过程:1.先建堆如下图:
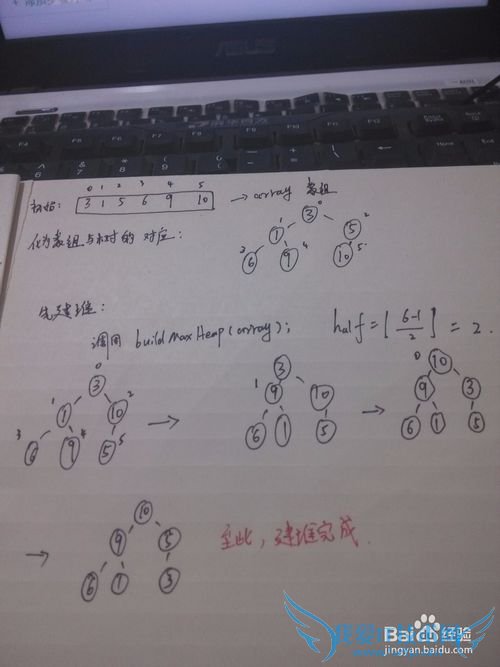
下面进行每次的迭代调堆,之后交换根与尾即可。


注意事项如果瞌睡的话就休息一下再看。经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。作者声明:本教程系本人依照真实经历原创,未经许可,谢绝转载。
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
