(2012？山东)如图，几何体E-ABCD是四棱锥，△ABD为正...

优质解答

(1)证明：∵四棱锥E-ABCD,底面△ABD为正三角形,CB=CD,

△BCD为等腰三角形

取BD中点O,连接AC,O在AC上

∵EC⊥BD

∴EO⊥底面于O,AC⊥BD

∴△BED为等腰三角形

∴EB=ED

(2)证明：∵∠BCD=120°,M为线段AE的中点

过D作DF⊥AB于F,F为AB中点

连接DM,MF

由（1）可知∠DBC+∠DBA=90°

∴BC⊥AB==>BC//DF

∴MF//BE

∴面DMF//面BCE

∵DM∈面DMF

∴DM//平面BEC

其他回答

证明：①连接AC，交BD于O，连接OE，△ABD为正三角形，则AB=AD

又 在平面ABCD中，CB=CD，即 A,C都在BD的垂直平分线上，

则 AC⊥BD 且 O为BD中点 又 EC⊥BD(已知) AC∩EC=C

∴ BD⊥平面ACE 则 BD⊥OE ...

其他类似问题

问题1：如图,在平行四边形ABCD中,E、F分别是为边ABCD的中点,BD是对角线,过A点作AG平行DB交CB的延长线于点G （2）若角G=90°,求证四边形DEBF是菱形.[数学科目]

ABCD是平行四边形

∴AD=CB

AB=CD

角DAE=角C

∵E、F分别是为边ABCD的中点

∴AE=CF

∴△AED≌△CFB

∴DE=BF

又∵BE=DF

∴四边形DEBF是平行四边形

∵AD∥CG,AG∥BD,∠G=90°

∴四边形ADBG是矩形

AB 是矩形的对角线,E是对角线的中点

∴DE也在矩形的对角线上

∴DE=EB（矩形对角线互相平分且相等）

∴四边形DEBF是菱形

问题2：在四面体ABCD中,BD=根号2a AB=AD=CB=CD=AC=a 如图,求证平面ABD垂直于平面BCD[数学科目]

取BD的中点E,连接AE、CE.

已知,BD = √2a ,AB = AD = a ,

可得：△ABD是等腰直角三角形,AE是斜边上的中线,

则有：AE⊥BD ,AE = (1/2)BD = (√2/2)a .

已知,BD = √2a ,CB = CD = a ,

可得：△CBD是等腰直角三角形,CE是斜边上的中线,

则有：CE = (1/2)BD = (√2/2)a .

已知,AC = a ,AE = CE = (√2/2)a ,

可得：△ACE是等腰直角三角形,

则有：AE⊥CE .

因为,AE⊥BD ,AE⊥CE ,BD和AE都在平面BCD内,

所以,AE⊥平面BCD ,而且,AE在平面ABD内,

可得：平面ABD⊥平面BCD .

问题3：如图，四面体ABCD中，O、E分别为BD、BC的中点，且CA=CB=CD=BD=2，AB=AD=2． （1）求证：AO⊥平面BCD；（2）求异面直线AB与CD所成角的余弦值．[数学科目]

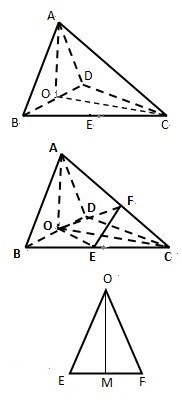（1）证明：△ABD中
∵AB=AD=2

，O是BD中点，BD=2
∴AO⊥BD 且 AO=A

B

2

-B

O

2

=1
△BCD中，连结OC∵BC=DC=2
∴CO⊥BD 且 CO=B

C

2

-B

O

2

=3

△AOC中 AO=1，CO=3

，AC=2
∴AO ²+CO²=AC² 故 AO⊥CO
∴AO⊥平面BCD
（2）取AC中点F，连结OF、OE、EF
△ABC中 E、F分别为BC、AC中点
∴EF∥AB，且 EF=12AB=22

△BCD中 O、E分别为BD、BC中点
∴OE∥CD 且 OE=12CD=1

∴异面直线AB与C D所成角等于∠OEF（或其补角）
又OF是Rt△AOC斜边上的中线
∴OF=12AC=1

∴等腰△OEF中 cos∠OEF=12EFOE=24

．

问题4：如图,在梯形ABCD中,AD‖CB,AD=2,BC=8,AC=6,BD=8,求梯形ABCD的面积.[数学科目]

平移AC,使A与D重合,C平移到了C‘ 此时AC’的平方+BD的平方=BC'的平方 所以AC'⊥BD,所以AC⊥BD 梯型面积就等于AC×BD×?=24

问题5：（2012?天津）如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1．（1）证明：PC⊥AD；（2）求二面角A-PC-D的正弦值；（3）设E为棱PA上的点,满足异面直线BE与CD所成的角为30°[数学科目]

我看不到啦