同学们提问关于“g-dian_如图AB BC CD分别与圆O切于E F G 且AB平行CD 连接OB ...[数学]”的问题,52IJ师说平台通过网络上精心整理了以下关于“g-dian_如图AB BC CD分别与圆O切于E F G 且AB平行CD 连接OB ...[数学]”的一些有用参考答案。请注意:文中所谈及的内容不代表本站的真正观点,也请不要相信各种联系方式。下面是本网所整理的“g-dian_如图AB BC CD分别与圆O切于E F G 且AB平行CD 连接OB ...[数学]”的相关信息:
如图AB BC CD分别与圆O切于E F G 且AB平行CD 连接OB ...
科目:数学 关键词:g-dian如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
(1)求证:MN是⊙O的切线;
(2)当0B=6cm,OC=8cm时,求⊙O的半径及MN的长
证明:(1)∵AB、BC、CD分别与⊙O切于点E、F、G
∴∠OBC= 1/2∠ABC,∠DCB=2∠DCM
∵AB∥CD
∴∠ABC+∠DCB=180°
∴∠OBC+∠OCB= 1/2(∠ABC+∠DCB)= 1/2×180°=90°
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°
∵MN∥OB
∴∠NMC=∠BOC=90°
∴MN是⊙O的切线
(2)连接OF,则OF⊥BC
由(1)知,△BOC是Rt△
∴ BC=根号下DB的平方+OC的平方=62+82=10
∵S△BOC= 1/2?OB?OC= 1/2?BC?OF
∴6×8=10×OF
∴0F=4.8cm
∴⊙O的半径为4.8cm
由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°
∴△NMC∽△BOC
∴ MN/OB=CM/CO即 MN/6=8+4.8/8
∴MN=9.6(cm)
其他类似问题
问题1:如图,AB,BC,CD分别与圆O切于点E,F,G,且AB平行CD.连接OB,OC,延长CO交圆O与点M,过点M作MN平行OB交CD于点N,[数学科目]
1,连OF,则OF⊥BC
∵AB‖CD
∴∠ABC+∠BCD=180°
∵AB BC CD分别与圆O切于E F G
∴∠ABO=∠CBO=1/2∠ABC,∠BCO=∠DCO=1/2∠BCD
∴∠CBO+∠OCB=90°
∴∠BOC=90°
∵MN‖OB
∴∠NMO=∠MOB=90°
∴MN是圆O的切线
2.∵∠BOC=90°
∴BC=√36+64=10.
∵△OBF∽△CBO
∵OF*BC=OB*OC
∴半径OF=48/10=4.8
∵∠FCO=∠NCM,∠OFC=∠NMC
∴△CMN∽△COF
∵NM,NG均是圆O的切线
∴NM=NG
设NM=NG=X,由△CMN∽△COF 得MN:OF=CN:CF
又CG=CF=√OC^2-OF^2=6.4
∴CN=6.4+X
故:X:4.8=(6.4+X):6.4
得MN=X=19.2cm
问题2:如图,AB,BC,CD分别与圆O相切于点EFG,且AB||CD,OB与EF相交于点M,OC与FG相交于点N,连接MN,求OB⊥OC[数学科目]
这样做的.
∵AB||CD,且AB切圆O于E,DC切圆O于G,
∴E、O、G三点共线,EG为圆O的直径,
∴∠EFG=90°
又∵BC为圆O切线
∴BO垂直平分EF,同理可得OC垂直平分FG
∴根据定义可知ONFM为矩形,MN=OF,角O=90°,BC=根号(BO2+OC2)=10
连接OF,则OF⊥BC,∠C为公共角,所以△CFO∽△COB,OF*BC=BO*OC
∴OF=BO*OC/BC=6*8/10=4.8
∴MN=4.8
懂了吗?
问题3:如图,AB,CD是圆O的直径,且AB⊥CD,E是OC的中点,过点E做FG平行AB ,交圆O于点F,G两点,求证:∠CBF=∠ABF[数学科目]
证明:因为FG平行AB,AB垂直CD
所以FG垂直OC
因为E为OC中点,
所以FG垂直平分OC
所以OF=CF
因为OF=OC
所以OF=CF=OC
所以三角形OCF是正三角形
所以∠COF=60度
∠CBF=1/2∠COF=30度
∠AOF=90-∠COF=30度
∠ABF=1/2∠AOF=15度
∠CBF=2∠ABF
可能会在图上出差错,有问题hi聊
问题4:如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC. (1)求证:∠ACO=∠BCD;(2)若EB=8cm,CD=24cm,求⊙O的直径.[数学科目]
 (1)证明:连接OC,
(1)证明:连接OC,
∵AB为⊙O的直径,CD是弦,且AB⊥CD于E,
∴CE=ED,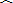 CB=
CB=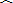 DB
DB
∴∠BCD=∠BAC.(3分)
∵OA=OC,∴∠OAC=∠OCA.
∴∠ACO=∠BCD.(5分)
(2)设⊙O的半径为Rcm,则OE=OB-EB=(R-8)cm,
CE=12CD=12×24=12cm,(6分)
在Rt△CEO中,由勾股定理可得
OC2=OE2+CE2,即R2=(R-8)2+122(8分)
解得R=13,∴2R=2×13=26cm.
答:⊙O的直径为26cm.(10分)
问题5:如图,AD是圆O的一条弦,B,C是弦AD上的点,AB=CD,连结OB,OC,分别延长OB,OC,交圆O于点(在线等,30分钟内)如图,AD是圆O的一条弦,B,C是弦AD上的点,AB=CD,连结OB,OC,分别延长OB,OC,交圆O于点E,F,求证:弧AE=弧DF[数学科目]
证明:连结OA、OD,
∵OA=OD=R,
∴△OAD是等腰△,
∴〈OAB=〈ODC,
∵OA=OD,
AB=CD,
∴△OAB≌△ODC,
∴〈AOE=〈DOF,
∴AE弧=DF弧.
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
