(2010年四川南充)已知抛物线 上有不同的两点E 和F .

精选知识

1证明：MN‖BC OEC=∠BCE E平分∠BCA ∠BCE=∠ACE

∴∠ECO=∠OEC E=OC 理OF=OC =FO

2当点O运动到AC中点时,四边形AECF是矩形

证明；易证∠ECF=90° OE=OF OA=OC∴四边形AECF是平行四边形

∴平行四边形AECF是矩形 .

其他回答

1)证明：MN‖BC ∴∠OEC=∠BCE ∵CE平分∠BCA ∴∠BCE=∠ACE

∴∠ECO=∠OEC ∴OE=OC 同理OF=OC ∴EO=FO

(2)当点O运动到AC中点时，四边形AECF是矩形

证明；易证∠ECF=90° OE=OF OA=OC∴四边形AECF是平行四边形

∴平行四边形AECF是矩形

其他类似问题

问题1：随着人们经济收入的不断提高及汽车产业的快速发展，汽车已越来越多地进入普通家庭，成为居民消费新的增长点．据某市交通部门统计，2008年底全市汽车拥有量为150万辆，而截止到2010年[数学科目]

（1）设该市汽车拥有量的年平均增长率为x（1分）
根据题意，得150（1+x）²=216（2分）
解得x₁=0.2=20%，x₂=-2.2（不合题意，舍去）．
答：该市汽车拥有量的年平均增长率为20%；（4分）
（2）设全市每年新增汽车数量为y万辆，则2011年底全市的汽车拥有量为216×90%+y万辆，2012年底全市的汽车拥有量为（216×90%+y）×90%+y万辆．
根据题意得（216×90%+y）×90%+y≤231.96，（6分）
解得y≤30；（7分）
答：该市每年新增汽车数量最多不能超过30万辆．（8分）

问题2：如图,在矩形ABCD中,AB=2,AD=3.点P是边AD上一点,联结CP,过点P作PF⊥CP交AB于F,以点C为圆心,CP长为半径作圆C,把圆C沿直线PF翻折得到圆C’.（1）如果圆C’与直线AB相切,求PD的长；（2）如果圆C’过点A,[数学科目]

1、过C‘作AB、AP的垂线交AB于G、交AP于H.

由翻折可得△C’HP≌△CDP.

∴HP=PD

又因为AB为⊙C’的切线,G为切点,所以C’G=CP=AH.

∵AD=AH+HP+PD=3,CP=√（PD²+2²）.

可设PD为x.

∴√（x²+4）+2x=3.

x²+4=4x²+4x+1.

3x²+4x-3=0

∴x=±（2+√13）/3.

∴PD=（2+√13）/3

2、圆C’过点A即A为AB切⊙C‘的切点.

所以可得点C’平分AP,AC‘=C’P.

由1证得C’P=PD,AC'+C‘P+PD=3,即3PD=3

∴PD=1.

问题3：初三数学题一道····[数学科目]

原式=(√x)^2-5√xy-6(√y)^2

=(√x-6√y)(√x+√y)

=0

∵x〉0,y〉0

∴√x-6√y=0

∴x=36y

∴代数式=(144y+6y+3y)/(324y+30y+6y)

=(153y)/(360y)

=17/40

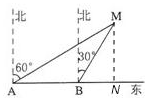
问题4：如图5,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60º方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30º方向上,那么该船继续航行____________分钟可使渔船到[数学科目]

你好,___醉千柔：

作MN⊥AB于N．

易知：∠MAB=30°,∠MBN=60°,

则∠BMA=∠BAM=30°．

设该船的速度为x,则BM=AB=0.5x．

Rt△BMN中,∠MBN=60°,

∴BN=1/2BM=0.25x．

故该船需要继续航行的时间为0.25x÷x=0.25小时=15分钟．

如图：

问题5：如图所示,有一块形状是直角梯形的铁皮ABCD,它的上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm,现要截出一块矩形铁皮MPCN,使它的顶点M.P.N分别在AB.BC.CD上（1）设MN为x,矩形MPCN的面积为S,求S关于X的函数[数学科目]

(1)过点A向BC作AE⊥BC,交MN于点F

∵MN‖BC

∴△AMF∽△ABP

∴MF/BP=AF/AP

即 x-3/5=(6-EF)/6

EF=(48-6x)/5

∴S=x*(48-6x)/5

=-[(6x²-48x)/5]=-（6/5）x²+（48/5)x

(2)当MN=-b/2a=4时有最大值（4ac-b²）/4a=96/5