欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“递归函数例子_能否给我一些关于一次函数的例题我想学学,不能少于10...[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
1 外部函数是指________的函数,它可以在_________中被调用.
【分析】当存储类型选用“extern”时,所定义的函数称为外部函数.外部函数可以在其他编译单位中调用(需要对这个函数进行说明).
【答案】存储类型是“extern”的函数
所有对该函数进行说明过的编译单位
2 假定在同一个编译单位中,函数a()调用了函数b(),则对函数b()不需要说明的情况有下列两种:_____________和________________.
【分析】教材中有明确答案(p116).
【答案】b()函数的定义地点在a()函数定义地点之前
b()函数的数据类型是int或char
3 在函数间传递数据的四种方式中,不能把被调函数的数据带回到主调函数的是()
①值传递 ②地址传递 ③返回值传递 ④全局外部变量
【分析】值传递方式是利用形式参数和实际参数结合来进行数据传递的一种方式,它是在调用函数时,将实际参数的值传递给形式参数,函授调用结束后,并不将形式参数的当前值传回实际参数.
【答案】①
4 如果函数定义时,形式参数是整型变量,则调用该函数时,实际参数不可以是()
①整型常量 ②字符型变量
③指向整型变量的指针型变量 ④整型表达式
【分析】当形式参数是变量时,实际参数可以是数据类型相同的表达式(常量、变量是表达式的特例),因此,备选答案①④显然是正确的,即不符合题意.而字符型数据可以看成整型数据,所以字符型变量可以当作整型变量,因此备选答案②也是正确的,即不符合题意.只有备选答案③是错误的,因为指针型变量不是整型变量,本题答案应该选取③.
请读者注意,如果使用“*指针型变量”侧是正确的.
【答案】③
5 若函数a()调用了函数b(),而函数b()又调用了函数a(),这样的调用称为_________________调用.
【分析】一般来说,只要是函数调用了自己,则称这样的函数调用为递归调用.如果函数f()调用了函数f(),我们称这样的递归调用为“直接递归调用”;如果函数f()调用了函数g(),而函数g()又调用了函数f(),这样的递归调用称为“间接递归调用”.
【答案】递归(或间接递归)
6 下列表达式中,不能判断字符型变量ch中的字符是英文字母(是则表达式值为非0、否则表达式值为0)的表达式是()
①ch>='A'&&ch<='Z'::ch>='a'&&h<='z'
② toupper(ch)>='A'&&toupper(ch)<='Z'
③ isalpha( ch)
④ !(isdigit(ch))
【分析】备选答案①中的逻辑表达式的含义是:当ch中的字符是大写字母或者小写字母时,结果为1,否则结果为0,该答案不符合题意.备选答案②中使用了系统函数toupper(),该函数功能是将参数对应的字符换成大写字母(如果参数对应的字符不是英文字母则不改变),答案中的逻辑表达式含义是:转换成大写后如果落在'A'到‘Z'之间则值为1,否则值为0.该答案也不符合题意.备选答案③中使用了系统函数isalpha(),该函数功能是判断参数对应的字符是否是英文字母,是则返回非0;否则返回0.显然该答案也不符合题意.只有备选答案④是符合题意的.分析这个答案中的表达式,其中用到了系统函数isdigit(),该函数的功能是判断参数对应的字符是不是数字字符,是则返回非 0,否则返回 0,该答案中的表达式是“! isdigit(ch)”,即 ch中不是数字字符则返回1,否则返回0,因此,该表达式不能判断ch中是否英文字母,所以本题答案应选④.
【答案】④
7 函数调用malloc(sizeof(long)* 2)的功能是申请____________个字节的内存;这批内存的首地址是____________________.
【分析】 系统池数malloc(形参)的功能是申请“形参”个字节的内存,函数的返回值就是这批内存的首地址.题目中的参数是“snzeof(long)*2”,sizeof(long)是长整型数据的字节数,其值为 4.而函数malloc(sizeof(long)* 2)调用的参数是 sizeof(long)* 2,其值为 8.
【答案】 8
函数调用的返回值
8 下列函数定义中,正确的是()
①int f(int x,y) ② int *f(int x,int*y)
{return(y);} { return(y);}
③ int f( x,*y) ④ void f( int x;)
int x, int y; {return(x);}
{return;}
【分析】分析备选答案①:形式参数表不正确,两个整型变量应该写成 int x,int y.分析备选答案②:这是一个指针型函数,函数返回值是指向整型数据的指针值,形式参数表也是正确的,在函数体中有带返回值的返回语句,且返回值就是指向整型数据的指针变量值,该答案符合题意.分析备选答案③:形式参数表中的int *y是错误的,应该为int y;这样形式参数说明中的 int y也是错误的,应该写成 int *y;函数体中的返回语句也是错误的,因为这个函数是有返回值的函数.分析备选答案④:形式参数表中最后的“分号”不能有 ;函数体中的返回语句只能用“ return;”,因为该函数是无返回值的函数.9 已知梯形法求积分y=|a f(x)dx的公式如下:
n-1
y=((f(a)+f(b))/2+∑f(a+ih)) )h
i=1
其中的n是积分区间等分的间隔数目(n是任选的,越大则结果精度越高);其中的h=(b-a)/n.
函数y()是计算并返回 |a(sin(x)+cos(x))dx积分值的,请填写函数中缺少的句.
# include"math.h"
double y(a,b,n)
double a, b;
int n;
{ double sum,h;
____________________
int i;
h=(b-a)/n;
sum=(f(a)+f(b))/2;
for(i=l;i<n;i++)
sum+= f(a+ i*h);
____________________
return( sum);
}
double f(x)
double x;
{ double y;
y=(sin(x)+cos(x));
return(y);
}
【分析】阅读程序清单可以看出函数 f()是求函数 f(X)= Sin()+ COS()值的,这个函数是完整的,没有要填写的语句.再看函数y(),这个函数是求积分的函数,其中有两个空白处.第1个空白处的前后都是数据定义语句,所以这个空白只能填写数据定义语句(包括数据、函数的说明语句).再从函数体中使用的数据来看,凡是用到的变量要么是形式参数(a、b、n),要么是定义的局部变量(sum、h、i),不存在没有定义的变量,对于这种情况来说,需要考虑函数体中调用的函数是否需要说明.从函数体中看出,要调用的函数是f(),这个函数的定义在调用处之后出现,并且不是int或char型(是double型),所以这儿的空白要填写对函数f()的说明.第2个空白处是在循环语句之后.分析这段程序,循环前先计算出h=(b-a)/n,再计算y=(f(a)+f(b)/2)(程序中用的变量是sum).接下来的次数
n-1
型循环显然是计算 ∑ f(a+ih),并且加到变量 sum中.
i=1
从题目给出的公式中可以看出,现在变量sum中的值还不是积分值,需要再乘以h,第 2个空白处就是完成这项工作的,所以应该填写的语句是 sum= sum* h;,或者 sum*=h;.
【答案】double f();
sum=sum*h; 或者 sum*=h;
10 求两个正整数的最大公约数的算法通常使用“辗转相除法”.设有两个正整数m、n,求它们的最大公约数的算法如下:
①若m<n,则交换m和n(保证m大于n).
②计算m/n的余数r.
③若r不等于0,则令m=n、n=r,转第②步继续执行;
否则,算法结束,n就是最大公约数.
下面就是用“辗转相除法'才出并返回m、n最大公约数的函数fmn(),请填写清单中缺少的语句.
int fmn( m, n)
int m, n;
{ int r;
if(m<n )
{r=m;m=n;n=r;}
if(n==0)
return(m);
do{_________________
if(r!= 0)
{ m=n; n=r;}
}while(r!=0);
return(n);
}
【分析】由于算法步骤已经给出,按照算法来理解程序就比较简单.函数体开始的单分支语
句是确保m值是大于n值的.接下来的单分支语句是确保算法中的除法“m/n”时的除数n不为0.注意,如果一开始的n就是O,则两个最大公约数就是m,此处利用返回语句返回的函数值就是m.接下来的do-while循环是实现算法步骤中的第②步和第③步的,显然该循环体中的第2条单分支语句是完成算法步骤中的第③步工作的,而空白处应该完成算法步骤中的第②步工作,即r等于m/n的余数.
【答案】r=m%n;
【说明】求最大公约数和最小公倍数的算法是常用算法;但在教材中并没有给出,希望读者在
学有余力的情况下,能掌握这两个算法.
求两个正整数的最小公倍数的算法在教材中也没有给出,下面给出求最小公倍数的一种算法.设有两个正整数m、n,求它们的最小公倍数的算法如下:
①若m<n,则交换m和n(保证m大于n).
②令d=m.
③若d能被n整除,则算法结束,d就是m和n的最小公倍数.
否则,令d=d+m,转第③步,继续执行.
实现算法的程序清单如下:
main()
{ int m, n, d ;
scanf("%d,%d",&m,&n);
if(m<n)
{ d=m;m=n;n=d;}
if(n==0)
d=0;
else
{ d=m;
while(d%n!=0)
d+=m;
}
printf(”%d\n”,d);
}
其他回答
空洞1 是我见过最幽默的人了。。。C语言?,哈哈^_^
其他类似问题
问题1:有关一次函数的习题 十道 最好是填空题[数学科目]
1、8分之5的10分之9是( )答案是( 16分之9 ) 2,、 30千克的5分之4是( )千克 答案是(24 ) 3、40分=( )时 答案是(3分之2)时 4、甲、乙两数的比是5:7,甲数是20,乙数是( ) 答案是(28) 5、货车的速度比客车慢4分之1,则货车速度与客车速度比是( ):( ) 答案是(3 ):(4 ) 我只给你提供这些,剩下的自己解决吧
问题2:一次函数表达式例题[数学科目]
例1.一个弹簧,不挂物体时长12cm,挂上物体后会伸长,伸长的长度与所挂物体的质量成正比例.如果挂上3kg物体后,弹簧总长是13.5cm,求弹簧总长是y(cm)与所挂物体质量x(kg)之间的函数关系式.如果弹簧最大总长为23cm,求自变量x的取值范围.分析:此题由物理的定性问题转化为数学的定量问题,同时也是实际问题,其核心是弹簧的总长是空载长度与负载后伸长的长度之和,而自变量的取值范围则可由最大总长→最大伸长→最大质量及实际的思路来处理.由题意设所求函数为y=kx+12
则13.5=3k+12,得k=0.5
∴所求函数解析式为y=0.5x+12
由23=0.5x+12得:x=22
∴自变量x的取值范围是0≤x≤22
问题3:什么是一次函数,举个例子[数学科目]
函数概念
在某一个变化过程中,设有两个变量x和y,如果可以写成y=f(x),(即x经过某种运算得到y),即每一个x都有唯一一个y与之对应,那么我们就说y是x的函数,其中x是自变量,y是因变量(y随x的变化而变化的意思).如果有2个及以上个值的y与某个x对应,又或者没有y对应于某个x,那么y就不是x的函数.[1]
定义
一般地,形如y=kx+b(k≠0,k,b是常数),那么y叫做x的一次函数.当b=0时,y=kx+b即y=kx,即正比例函数(自变量和因变量成正比例).所以说正比例函数是一种特殊的一次函数,但不能说一次函数是正比例函数.
若自变量最高次数为1,则这个函数就是一次函数.
还有一种量,它的取值始终保持不变,我们称之为常量(如π).
表示方法
1、解析式法
用含自变量x的式子表示函数的方法.
2、列表法
把一系列x的值对应的函数值y列成一个表来表示的函数关系的方法叫做列表法.
3、图像法
用图像来表示函数关系的方法叫做图像法.
解析式
一次函数的解析式为:
其中k是比例系数,不能为0;x表示自变量.且k和b均为常数.
问题4:有关初中二元一次函数的例题及解析.[数学科目]
例题:{3x+y=-1
4x+2y=1
将X和Y的任意一个系数取两个式子的最小公倍数如:
方法一:给1式X4得:12x+4y=-4
给2 式X3得:12x+6y=3
有3式—4式=4y—6y=-4—3=-7
即:-2y=-7
得y=3.5
带入1式得x=-1.5
方法二:给1式X2将y统一得:
6x+2y=-2
用5式—2式得6X—4x=-2—1=-3
得x=-1.5
带入1式得y=3.5
问题5:请问数学的一次函数和反比例函数应该怎么学给我讲讲几个例题,教我一些学一次函数和反比例函数的好方法[数学科目]
一、一次函数:
在某一个变化过程中,设有两个变量x和y,如果可以写成y=kx+b(k为一次项系数k≠0,b为常数),那么我们就说y是x的一次函数,其中x是自变量,y是因变量.
1、函数的由来
中文数学书上使用的“函数”一词是转译词.是中国清代数学家李善兰在翻译《代数学》(1852年到1859年间)一书时,把“function”译成“函数”的.
中国古代“函”字与“含”字通用,都有着“包含”的意思.李善兰给出的定义是:“凡式中含天,为天之函数.”中国古代用天、地、人、物4个字来表示4个不同的未知数或变量.这个定义的含义是:“凡是公式中含有变量x,则该式子叫做x的函数.”所以“函数”是指公式里含有变量的意思.现代所说的方程的确切定义是指含有未知数的等式.但是方程一词在中国早期的数学专著《九章算术》中,意思指的是包含多个未知量的联立一次方程,即线性方程组.
2、基本定义
定义
一般地,形如y=kx+b(k≠0,k,b是常数),那么y叫做x的一次函数.当b=0时,y=kx+b即y=kx,即正比例函数(自变量和因变量成正比例).所以说正比例函数是一种特殊的一次函数.
还有,若自变量最高次数为1,则这个函数就是一次函数.
在某一个变化过程中,设有两个变量x和y,如果可以写成y=f(x),(即x经过某种运算得到y),即每一个x都有唯一一个y与之对应,那么我们就说y是x的函数,其中x是自变量,y随X的变化而变化.当x取一个值时,y有且只有一个值与x对应.如果有2个及以上个值与x对应时,就不是函数.表示法:函数常用的表示方法:解析法、图像法、列表法.
3、基本性质
1.在正比例函数时,x与y的商一定(x≠0).在反比例函数时,x与y的积一定.
在y=kx+b(k,b为常数,k≠0)中,当x增大m时,函数值y则增大km,反之,当x减少m时,函数值y则减少km.
2.当x=0时,b为一次函数图像与y轴交点的纵坐标,该点的坐标为(0,b).[2]
3.当b=0时,一次函数变为正比例函数.当然正比例函数为特殊的一次函数.[2]
4.在两个一次函数表达式中:
当两个一次函数表达式中的k相同,b也相同时,则这两个一次函数的图像重合;
当两个一次函数表达式中的k相同,b不相同时,则这两个一次函数的图像平行;
当两个一次函数表达式中的k不相同,b不相同时,则这两个一次函数的图像相交;
当两个一次函数表达式中的k不相同,b相同时,则这两个一次函数图像交于y轴上的同一点(0,b);
当两个一次函数表达式中的k互为负倒数时,则这两个一次函数图像互相垂直.[2]
5.两个一次函数(y1=ax+b,y2=cx+d)之比,得到的新函数y3=(ax+b)/(cx+d)为反比例函数,渐近线为x=-b/a,y=c/a.
4、特殊位置关系
当平面直角坐标系中两直线平行时,其函数解析式中k的值(即一次项系数)相等;
当平面直角坐标系中两直线垂直时,其函数解析式中k的值互为负倒数(即两个k值的乘积为-1)
注意:与y轴平行的直线没有函数解析式,与x轴平行的直线的解析式为常函数,故上述性质中这两种直线除外.
5、常见题型
常见题型一次函数及其图像是初中代数的重要内容,也是高中解析几何的基石,更是中考的重点考查内容.其中求一次函数解析式就是一类常见题型.现以部分中考题为例介绍几种求一次函数解析式的常见题型.希望对大家的学习有所帮助.
一. 定义型 例1. 已知函数 是一次函数,求其解析式. 由一次函数定义知 ,故一次函数的解析式为 注意:利用定义求一次函数 解析式时,要保证 .如本例中应保证
二. 点斜型 例2. 已知一次函数 的图像过点(2,-1),求这个函数的解析式. 一次函数 的图像过点(2,-1) ,即 故这个一次函数的解析式为 变式问法:已知一次函数 ,当 时,y=-1,求这个函数的解析式.
三. 两点型 已知某个一次函数的图像与x轴、y轴的交点坐标分别是(-2,0)、(0,4),则这个函数的解析式为_____________. 设一次函数解析式为 由题意得 故这个一次函数的解析式为
四. 图像型 例4. 已知某个一次函数的图像如图所示,则该函数的解析式为__________. 设一次函数解析式为 由图可知一次函数 的图像过点(1,0)、(0,2) 有 故这个一次函数的解析式为
五. 斜截型 例5. 已知直线 与直线 平行,且在y轴上的截距为2,则直线的解析式为___________. 解析:两条直线 : ; : .当 , 时, 直线 与直线 平行, . 又 直线 在y轴上的截距为2, 故直线的解析式为
六. 平移型 例6. 把直线 向下平移2个单位得到的图像解析式为___________. 解析:设函数解析式为 , 直线 向下平移2个单位得到的直线 与直线 平行 直线 在y轴上的截距为 ,故图像解析式为 七. 实际应用型 例7. 某油箱中存油20升,油从管道中匀速流出,流速为0.2升/分钟,则油箱中剩油量Q(升)与流出时间t(分钟)的函数关系式为___________. 由题意得 ,即 故所求函数的解析式为 ( ) 注意:求实际应用型问题的函数关系式要写出自变量的取值范围.
八. 面积型 例8. 已知直线 与两坐标轴所围成的三角形面积等于4,则直线解析式为__________. 易求得直线与x轴交点为( ,0),所以 ,所以 ,即 故直线解析式为 或
九. 对称型 若直线 与直线 关于 (1)x轴对称,则直线l的解析式为 (2)y轴对称,则直线l的解析式为 (3)直线y=x对称,则直线l的解析式为 (4)直线 对称,则直线l的解析式为 (5)原点对称,则直线l的解析式为 例9. 若直线l与直线 关于y轴对称,则直线l的解析式为____________. 由(2)得直线l的解析式为
十. 开放型 例10. 已知函数的图像过点A(1,4),B(2,2)两点,请写出满足上述条件的两个不同的函数解析式,并简要说明解答过程. (1)若经过A、B两点的函数图像是直线,由两点式易得 (2)由于A、B两点的横、纵坐标的积都等于4,所以经过A、B两点的函数图像还可以是双曲线,解析式为
二、反比例函数1、形如函数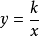 (k为常数且k≠0)叫做反比例函数,其中k叫做反比例系数,x是自变量,y是自变量x的函数,x的取值范围是不等于0的一切实数,且y也不能等于0.k大于0时,图像在1、3象限.k小于0时,图像在2、4象限.k表示的是x与y的坐标形成的矩形的面积.
(k为常数且k≠0)叫做反比例函数,其中k叫做反比例系数,x是自变量,y是自变量x的函数,x的取值范围是不等于0的一切实数,且y也不能等于0.k大于0时,图像在1、3象限.k小于0时,图像在2、4象限.k表示的是x与y的坐标形成的矩形的面积.
2、自变量的取值范围
① 在一般的情况下 , 自变量 x 的取值范围可以是 不等于0的任意实数;
②函数 y 的取值范围也是任意非零实数.
3、解析式
其中x是自变量,y是x的函数,其定义域是不等于0的一切实数,
即 {x|x≠0,x∈R}.下面是一些常见的形式:
(k为常数(k≠0),x不等于0)
4、概述
反比例函数的图像属于以原点为对称中心的中心对称的双曲线,反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交(y≠0).
5、函数性质
单调性
当k>0时,图像分别位于第一、三象限,每一个象限内,从左往右,y随x的增大而减小;
当k<0时,图像分别位于第二、四象限,每一个象限内,从左往右,y随x的增大而增大.
k>0时,函数在x<0上同为减函数、在x>0上同为减函数;k<0时,函数在x<0上为增函数、在x>0上同为增函数.
相交性
因为在
(k≠0)中,x不能为0,y也不能为0,所以反比例函数的图像不可能与x轴相交,也不可能与y轴相交,只能无限接近x轴,y轴.
面积
函数性质
单调性
当k>0时,图像分别位于第一、三象限,每一个象限内,从左往右,y随x的增大而减小;
当k<0时,图像分别位于第二、四象限,每一个象限内,从左往右,y随x的增大而增大.
k>0时,函数在x<0上同为减函数、在x>0上同为减函数;k<0时,函数在x<0上为增函数、在x>0上同为增函数.
相交性
因为在
(k≠0)中,x不能为0,y也不能为0,所以反比例函数的图像不可能与x轴相交,也不可能与y轴相交,只能无限接近x轴,y轴.
6、概念理解
形如(k为常数且k≠0)的函数,叫做反比例函数.
自变量x的取值范围是不等于0的一切实数.
反比例函数图像性质:反比例函数的图像为双曲线.
由于反比例函数属于奇函数,有f(x)=f(-x),图像关于原点对称.
另外,从反比例函数的解析式可以得出,在反比例函数的图像上任取一点,向两个坐标轴作垂线,这点、两个垂足及原点所围成的矩形面积是定值,为∣k∣.
注:反比例函数图像只能无限趋向于坐标轴,无法和坐标轴相交.
7、重点知识
过反比例函数图象上任意一点作两坐标轴的垂线段,这两条垂线段与坐标轴围成的矩形的面积为|k|.
对于双曲线,若在分母上加减任意一个实数(,m为常数),就相当于将双曲线图象向左或右平移一个单位.(加一个数时向左平移,减一个数时向右平移)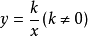
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
