选址问题_多目标优化选址问题两个目标函数的优化问题如何建模？...[数学]

精选知识

有两种办法：

1、加权求和法：比较两目标函数的主次,分别赋以一定的权重（权重和为1）,再用求和的方式将其化简为简单的线性规划问题.

2、主次分析法：就本题而言,比较两目标函数的主次,以主为目标函数,辅为约束条件,化简为简单的线性规划问题.

其他类似问题

问题1：数学建模（枢纽机场的选址问题）枢纽机场的选址问题要求：（1） 建立数学模型选择建立三个枢纽机场的地点并设计合理的航线网络；（2） 根据目前我国的西部大开发战略思想,若在西部

哎,这竞赛怎么越看越麽意思,说句实在点的话,几天通宵坐在电脑面前,两眼发晕在网上找资料,然后随便下了篇论文就胡乱改了几处就完事了.一切就为了个什么一等奖之类的.数学建模源于美国,可美国人却并不把它当回事,因为真正的科学研究源于兴趣和爱好,它是一个长久的过程,可能几年,也可能一辈子.而不是几天不吃不喝就能完事的.数模的训练其实就在枯竭中国大学生对于数学最原始的爱好与热情.在中国参加数模无非就是为了得奖,去找工作.这是数模的悲哀.!说实在的,有几个人真正觉得自己很感兴趣!

当然话说回来,数模培养出来的思维与团队协调能力还是值得肯定的.

桂电骷髅协会-----101AIRFORCE

问题2：A题：某厂准备将具有下列成分的几种现成合金混合起来,成为一种含铅30%,含心20%,含锡50%的新合金,有关数据如下表：表1 5种合金的成分与费用合金 A B C D E 含铅（％） 30 10 50 10 50 含锌（％） 6

利用到数学的线性规划.

设要用的合金A,B,C,D,E分别为a,b,c,d,e公斤

那么可以得到以下三个方程

0.3a+0.1b+0.5c+0.1d+0.5e=0.3(a+b+c+d+e)

0.6a+0.2b+0.2c+0.1d+0.1e=0.2(a+b+c+d+e)

0.1a+0.7b+0.3c+0.8d+0.4e=0.5(a+b+c+d+e)

我们不妨令a+b+c+d+e=1,因为题目所求的只是abcde的比值关系

那么上边的算式立刻少了一个未知数e

0.3a+0.1b+0.5c+0.1d+0.5(1-a-b-c-d)=0.3

0.6a+0.2b+0.2c+0.1d+0.1(1-a-b-c-d)=0.2

0.1a+0.7b+0.3c+0.8d+0.4(1-a-b-c-d)=0.5

现在有四个未知数,3条算式是不可能求得a,b,c,d的

但是注意到题目有费用最低的限制,就可以有：

y=8.5a+6.5b+8.9c+5.7d+8.8(1-a-b-c-d) 要最小

这个时候就比较棘手了,因为如果是只有两个未知数,建立平面直角坐标系就立刻出结果,但是这里有四个未知数,是一个四维的概念.所以要借助计算机去计算.

如果你想a,b,c,d的比列关系精确到0.01,你可以设计一个如下的循环的程序：

分别给a从0到1,每隔0.01赋值,

在每一个a的值中,又对b进行如下的操作

在每一个b的值中,又对c进行如下的操作

又1-a-b-c求得d的值

计算y

重复100*99*98次,找出y最小值对应的a,b,c,d即可.

这时e也出来了.

问题3：数学建模的规划方法都有哪些啊?每种规划都有什么特点?适合什么问题的应用?知道的说下,[语文科目]

可以分为：按是否线性可分为线性规划和非线性规划,一次是线性的,其他就是非线性的,按是否份过程阶段 分动态规划和非动态规划,按目标函数的多少分,可以分单目标规划和多目标规划 .

线性和非线性的比较常见,我说说其他的吧.

动态规划(dynamic programming)是运筹学的一个重要分支,它是解决多阶段决策问题的一种有效的数量化方法.动态规划是由美国学者贝尔曼(R.Bellman)等人所创立的.1951年贝尔曼首先提出了动态规划中解决多阶段决策问题的最优化原理,并给出了许多实际问题的解法.1957年贝尔曼发表了《动态规划》一书,标志着运筹学这一重要分支的诞生.

动态规划从创立到现在五十多年来,无论在工程技术,企业管理还是在工农业生产及军事等部门都有广泛的应用,并获得了显著的效果.在管理方面,动态规划可用于资源分配问题,最短路径问题,库存问题,背包问题,设备更新问题,最优控制问题等等.所以动态规划是现代管理学中进行科学决策不可缺少的工具.

动态规划的优点在于,它把一个多维决策问题转化为若干个一维最优化(optimization)问题,而对一维最优化问题一个一个地去解.这种方法是许多求极值方法所做不到的,它几乎优于所有现存的优化方法.除此之外,动态规划能求出全局极大或极小,这一点也优于其他优化方法.需要指出的是,动态规划是求解最优化问题的一种方法,是解决问题的一种途径,而不是一种新的算法.在前面我们学习了用单纯形解线性规划问题,凡是具有线性规划问题那样统一的数学模型都可以用单纯形法去求解,而动态规划问题的求解却没有统一的方法(类似于单纯形法).因此在用动态规划求解最优化问题中,必须对具体问题具体分析,针对不同的问题,使用动态规划的最优化原理(optimization principle)和方法,建立起与其相应的数学模型,然后再用动态规划方法去求解.根据动态规划这些特点,要求我们在学好动态规划的基本原理和方法的同时,还应具有丰富的想象力,只有这样才能建好模型求出问题的最优解.

可根据时间变量是离散的还是连续的,把动态规划问题的模型分为离散决策过程和连续决策过程,根据决策过程的演变是确定性的还是随机性的,动态规划问题的模型又可分为确定性的决策过程和随机性的决策过程,即离散确定性,离散随机性,连续确定性,连续随机性四种决策过程模型.我们主要研究离散确定性模型.

2.随机规划和模糊规划是处理随机和模糊优化问题的两大数学规划工具,称之为不确定规划.主要目的是为不确定环境中的优化理论奠定一个基础.不确定规划理论由三大类组成：期望值模型,机 会约束规划和相关机会规划.

3.随机规划的概念比较少见

可以参考一下运筹学的分支

数学规划的研究对象是计划管理工作中有关安排和估值的问题,解决的主要问题是在给定条件下,按某一衡量指标来寻找安排的最优方案.它可以表示成求函数在满足约束条件下的极大极小值问题.

数学规划和古典的求极值的问题有本质上的不同,古典方法只能处理具有简单表达式,和简单约束条件的情况.而现代的数学规划中的问题目标函数和约束条件都很复杂,而且要求给出某种精确度的数字解答,因此算法的研究特别受到重视.

这里最简单的一种问题就是线性规划.如果约束条件和目标函数都是呈线性关系的就叫线性规划.要解决线性规划问题,从理论上讲都要解线性方程组,因此解线性方程组的方法,以及关于行列式、矩阵的知识,就是线性规划中非常必要的工具.

线性规划及其解法—单纯形法的出现,对运筹学的发展起了重大的推动作用.许多实际问题都可以化成线性规划来解决,而单纯形法有是一个行之有效的算法,加上计算机的出现,使一些大型复杂的实际问题的解决成为现实.

非线性规划是线性规划的进一步发展和继续.许多实际问题如设计问题、经济平衡问题都属于非线性规划的范畴.非线性规划扩大了数学规划的应用范围,同时也给数学工作者提出了许多基本理论问题,使数学中的如凸分析、数值分析等也得到了发展.还有一种规划问题和时间有关,叫做“动态规划”.近年来在工程控制、技术物理和通讯中的最佳控制问题中,已经成为经常使用的重要工具.

排队论是运筹学的又一个分支,它有叫做随机服务系统理论.它的研究目的是要回答如何改进服务机构或组织被服务的对象,使得某种指标达到最优的问题.比如一个港口应该有多少个码头,一个工厂应该有多少维修人员等.

排队论最初是在二十世纪初由丹麦工程师艾尔郎关于电话交换机的效率研究开始的,在第二次世界大战中为了对飞机场跑道的容纳量进行估算,它得到了进一步的发展,其相应的学科更新论、可靠性理论等也都发展起来.

因为排队现象是一个随机现象,因此在研究排队现象的时候,主要采用的是研究随机现象的概率论作为主要工具.此外,还有微分和微分方程.排队论把它所要研究的对象形象的描述为顾客来到服务台前要求接待.如果服务台以被其它顾客占用,那么就要排队.另一方面,服务台也时而空闲、时而忙碌.就需要通过数学方法求得顾客的等待时间、排队长度等的概率分布.

排队论在日常生活中的应用是相当广泛的,比如水库水量的调节、生产流水线的安排,铁路分成场的调度、电网的设计等等.

对策论也叫博弈论,前面讲的田忌赛马就是典型的博弈论问题.作为运筹学的一个分支,博弈论的发展也只有几十年的历史.系统地创建这门学科的数学家,现在一般公认为是美籍匈牙利数学家、计算机之父——冯·诺依曼.

最初用数学方法研究博弈论是在国际象棋中开始的——如何确定取胜的着法.由于是研究双方冲突、制胜对策的问题,所以这门学科在军事方面有着十分重要的应用.近年来,数学家还对水雷和舰艇、歼击机和轰炸机之间的作战、追踪等问题进行了研究,提出了追逃双方都能自主决策的数学理论.近年来,随着人工智能研究的进一步发展,对博弈论提出了更多新的要求.

搜索论是由于第二次世界大战中战争的需要而出现的运筹学分支.主要研究在资源和探测手段受到限制的情况下,如何设计寻找某种目标的最优方案,并加以实施的理论和方法.在第二次世界大战中,同盟国的空军和海军在研究如何针对轴心国的潜艇活动、舰队运输和兵力部署等进行甄别的过程中产生的.搜索论在实际应用中也取得了不少成效,例如二十世纪六十年代,美国寻找在大西洋失踪的核潜艇“打谷者号”和“蝎子号”,以及在地中海寻找丢失的氢弹,都是依据搜索论获得成功的.

运筹学有广阔的应用领域,它已渗透到诸如服务、库存、搜索、人口、对抗、控制、时间表、资源分配、厂址定位、能源、设计、生产、可靠性、等各个方面.

应该排队论和随机规划是比较接近的

具体的还希望你问一下专业的老师

希望对你有帮助

问题4：油管铺设某石化公司要铺设一根石油管道,将石油从炼油厂输送到河对岸的石油灌装点,如图所示.炼油厂附近有条宽2.5km的河,灌装点在炼油厂对岸沿河下游10km处.如果在水中铺设管道的费用为6[数学科目]

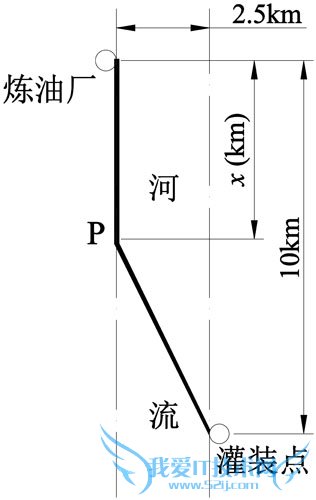
如上图铺设管道.

设：P点位于炼油厂下游x（km）处,0≤x≤10.铺设的总费用是y万元.

依题意和已知,有：

y=4x+6√[2.5²+(10-x)²]

y=4x+6√(x²-20x+106.25)

y'=4+3(2x-20)/√(x²-20x+106.25)

y'=[4√(x²-20x+106.25)+6x-60]/√(x²-20x+106.25)

1、令：y'＞0,即：[4√(x²-20x+106.25)+6x-60]/√(x²-20x+106.25)＞0

有：2√(x²-20x+106.25)+3x-30＞0

30-3x＜2√(x²-20x+106.25)

9x²-180x+900＜4(x²-20x+106.25)

x²-20x+95＜0

(x-10)²＜5

10-√5＜x＜10+√5

因为：0≤x≤10,

所以：当10-√5＜x≤10时,y是单调增函数；

2、令：y'＜0,即：[4√(x²-20x+106.25)+6x-60]/√(x²-20x+106.25)＜0

有：2√(x²-20x+106.25)+3x-30＜0

30-3x＞2√(x²-20x+106.25)

9x²-180x+900＞4(x²-20x+106.25)

x²-20x+95＞0

(x-10)²＞5

x＞10+√5,或：x＜10-√5

因为：0≤x≤10,

所以：当0≤x＜10-√5时,y是单调减函数；

综上所述,有：

当x=10-√5（km）≈7.7639km时,y有极小值.

y极小=4(10-√5)+6√[(10-√5)²-20×(10-√5)+106.25]

=40-4√5+6√11.25

≈51.1803(万元)

答：当p点位于下游约7.7639km处时,所需费用最低.费用约是51.1803万元.

问题5：消防站选址问题（数学建模）十二个地点中,选三个地点,每个点上还有权.要求,十二个点到这个三个点的加权距离最短.距离矩阵v1 v2 v3 v4 v5 v6 v7 v8 v9 v10 v11 v12v1 0 15 37 45 24 60 18 33 48 40 58 67v2 15 0 [数学科目]

你的思路是可行的.用lingo数学优化软件,建立的模型代码：

model:

sets:

PL/1..12/:w,T;!T为决策变量,T(i)=1表示i点选择;

DS(PL,PL):d;

endsets

data:

w=15 10 12 18 5 24 11 16 13 22 19 20;

d=0 15 37 45 24 60 18 33 48 40 58 67

15 0 22 40 38 52 33 48 42 55 61 61

37 22 0 18 16 30 43 28 20 58 39 39

45 40 18 0 34 12 61 46 24 62 43 34

24 38 16 34 0 36 27 12 24 49 43 43

60 52 30 12 36 0 57 42 12 50 31 22

18 33 43 61 27 57 0 15 45 22 40 61

33 48 28 46 12 42 15 0 30 37 25 46

48 42 20 24 24 12 45 30 0 38 19 19

40 55 58 62 49 50 22 37 38 0 19 40

58 61 39 43 43 31 40 25 19 19 0 21

67 61 39 34 43 22 61 46 19 40 21 0;

enddata

min=@sum(PL(i):w(i)*@sum(PL(j):w(j)*d(i,j)*T(i)));!我认为加权值应为w1*w2*d12;

@for(PL:@bin(T));

@sum(PL:T)=3;

end

运行结果是：

加权最短距离是162380；

选择的3个点是v3、v5、v9.