正三棱锥的性质_在正三棱锥A

精选知识

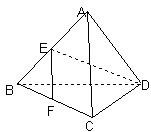∵EF∥AC，EF⊥DE
∴AC⊥DE
∵AC⊥BD（正三棱锥性质）
∴AC⊥平面ABD
所以正三棱锥A-BCD是正方体的一个角，AB=1，
从而得此正三棱锥的外接球即是相应的正方体的外接球，此正方体的面对角线为2

，边长为1．
正方体的体对角线是1+1+1

=3

．
故外接球的直径是3

，半径是32

．
故其体积是43π

R

3

=4π3×

(32)

3

=32π

．
故选B．

其他类似问题

问题1：在正三棱锥A-BCD中，E，F分别是AB，BC的中点，EF⊥DE且BC=2，若此正三棱锥的四个顶点都在球O的面上，则球O的体积是（　　）A. 36πB. 32πC. 33πD. 33π[数学科目]

∵EF∥AC，EF⊥DE
∴AC⊥DE
∵AC⊥BD（正三棱锥性质）
∴AC⊥平面ABD
所以正三棱锥A-BCD是正方体的一个角，AB=1，
从而得此正三棱锥的外接球即是相应的正方体的外接球，此正方体的面对角线为2

，边长为1．
正方体的体对角线是1+1+1

=3

．
故外接球的直径是3

，半径是32

．
故其体积是43π

R

3

=4π3×

(32)

3

=32π

．
故选B．

问题2：一个正方体的顶点都在球面上,它的棱长是a cm,求球的体积[数学科目]

正方体的对角线即为球的直径

由于对角线为√（a2+a2+a2）=√3a cm,

则球的半径R=1/2*√3a=√3/2a cm,

所以球的体积为V=4/3πR3=√3/2a3 cm3

问题3：表面积为23的正八面体的各个顶点都在同一个球面上，则此球的体积为 ___ ．[数学科目]

由题意表面积为23

的正八面体的各个顶点都在同一个球面上，故每个侧面三角形的面积都是34

且为等边三角形，设其边长为a，则有12×a×a×sin60°

=34

，解得a=1
故此四点组成的正方形的对角线的长为2

，球的半径是22

所以此球的体积为43 ×π×

(22)

3

=23π

故答案为23π

问题4：一个正方体的各顶点均在同一球面上,若该球的体积为4根号3派 则该正方体表面积为? 在线等[数学科目]

球体积：V＝4πR^3/3=4√3π

得R＝√3

这时球的直径2√3即是这个正方体的体对角线√3a（设正方体的村长为a）

故正方体的棱长为2

正方体的表面积为6·a^2＝24

问题5：一个正方体的顶点都在球面上，它的棱长为2cm，则球的体积是______．[数学科目]

因为一个正方体的顶点都在球面上，它的棱长为2cm，
所以正方体的外接球的直径就是正方体的对角线的长度：23

．
所以球的半径为：3

．
所求球的体积为：4π3

(3)

3

=43π

．
故答案为：43π

．