如图，已知直线l1∥l2∥l3∥l4，相邻两条平行直线间的...

精选知识

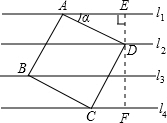过D作EF⊥l₁，交l₁于E，交l₄于F，
∵EF⊥l₁，l₁∥l₂∥l₃∥l₄，
∴EF和l₂，l₃，l₄的夹角都是90°，
即EF与l₂，l₃，l₄都垂直，
∴DE=1，DF=2．
∵四边形ABCD是正方形，
∴∠ADC=90°，AD=CD，
∴∠ADE+∠CDF=90°，
又∵∠α+∠ADE=90°，
∴∠α=∠CDF，
∵AD=CD，∠AED=∠DFC=90°，
∴△ADE≌△DCF，
∴DE=CF=1，
∴在Rt△CDF中，CD=

CF

2

+

DF

2

=5

，
∴sinα=sin∠CDF=CFCD

=15

=55

．
故选B．

其他类似问题

问题1：如图，已知直线l1∥l2∥l3∥l4，相邻两条平行直线间的距离都是1，如果正方形ABCD的四个顶点分别在四条直线上，则sinα=______．[数学科目]

过D作EF⊥l₁，交l₁于E，交l₄于F．
∵EF⊥l₁，l₁∥l₂∥l₃∥l₄，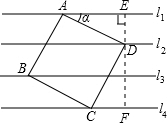
∴EF和l₂、l₃、l₄的夹角都是90°，
即EF与l₂、l₃、l₄都垂直，
∴DE=1，DF=2．
∵四边形ABCD是正方形，
∴∠ADC=90°，AD=CD，
∴∠ADE+∠CDF=90°．
又∵∠α+∠ADE=90°，
∴∠α=∠CDF．
∵AD=CD，∠AED=∠DFC=90°，
∴△ADE≌△DFC，
∴DE=CF=1，
∴在Rt△CDF中，CD=

CF

2

+

DF

2

=5

，
∴sinα=sin∠CDF=CFCD

=15

=55

．

问题2：平面内4条直线l1,l2,l3,l4是一组平行线,相邻两条距离都是1,正方形ABCD的4顶点A、B.C、D都在这些平行线上,其中A、C分别在直线l1,l4上,该正方形面积[数学科目]

如图 蓝色三角形≌黄色三角形﹙AAS﹚ 正方形面积＝边长2＝12+22＝5﹙面积单位﹚

[ 细节自己补充.O.K ? ]

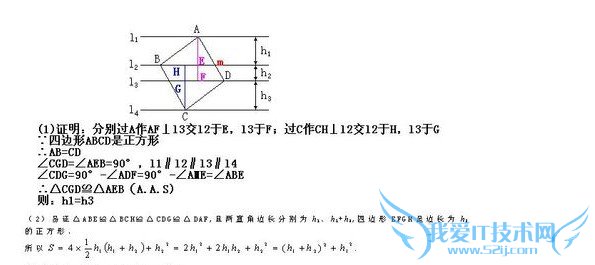
问题3：如图,正方形ABCD的四个顶点分别在四条平行线L1、L2、L3、L4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3（1）求证：h1=h3（2）设正方形ABCD的面积为S,求证：S=（h1+h2）2+h12[数学科目]

（1）设AD、BC与l2、l3相交于点E、F.

由题意知四边形BEDF是平行四边形,

∴△ABE≌△CDF（ASA）.

∴对应高h1＝h3.

(2)过B、D分别作l4的垂线,交l4于G、H（如图）,

易证△BCG≌△CDH,从而根据勾股定理,得

CB2＝BG2＋GC2＝BG2＋HD2,

即：S＝(h3＋h2)2＋h32＝(h1＋h2)2＋h12.

问题4：如图,正方形ABCD边长为5,直线L1平行于L2平行于L3平行于L4,且直线L2和直线L3之间的距离为1如果正方形ABCD的四个顶点分别在四条直线上.（1）证明三角形AED全等于三角形CFB（2）求直线L1与L2之间

右边的E为D,

(1)

AD=BC=AB=CD=5

L1平行于L2平行于L3平行于L4,ABCD为正方形,

AB平行于CD,所以BFDE为平行四边形,DE=BF,BE=FD

AE=AB-BE=CD-BE=CD-FD=CF,

三角形AED全等于三角形CFB,[SSS]

(2)

作EM⊥BF于M,设BE=X;

作AG⊥BF于G,交ED于N,EM=NG=1;

AN=h,AG=AN+NG=h+1,

BE:BA=EM:AG

X:5=1：(h+1)

h=(5-X)/X

RT△ANE∽RT△DAE,

AE:ED=AN:AD

(AB-EB):ED=h:5

(5-X):ED=(5-X)/X:5

ED=5X；

角A=90°,

ED2=AE2+AD2

25X2=(5-X)2+52

25X2=25-10X+X2+25

12X2+5X-25=0

(4X-5)(3X+5)=0

X1=5/4,X2=-5/3(舍去)

h=(5-X)/X=(5-5/4)/(5/4)=3

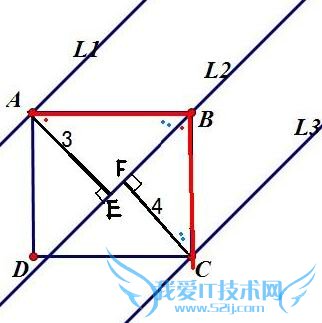
问题5：如图,直线L1,L2,L3分别过正方形ABCD的三个顶点A,B,C,且相互平行,若L1、L2距离为3,L2、L3距离为4,则正方形ABCD的面积是——（答案是25,）.[数学科目]

如图,作AE⊥L2 CF⊥L2 则AE＝3 CF＝4 又⊿AEB≌⊿BFC﹙ASA﹚ ∴BE＝CF

方形ABCD的面积＝AB2＝AE2+EB2＝AE2+FC2＝32+42＝25