如图，点P是正方形ABCD边AB上的一点(不与点A、B重合)，...

精选知识

（1）证明:PE垂直PD,则∠EPB+∠APD=90°;

又∠ADP+∠APD=90°.

所以,∠ADP=∠EPB.

在AD上截取线段AQ=AP,连接PQ,则DQ=PB;∠AQP=∠APQ=45°,∠DQP=135°.

又PD=PE;∠ADP=∠EPB.

故⊿DQP≌⊿PBE,∠PBE=∠DQP=135°,

所以∠CBE=45°.

（3)假设△PFD∽△BFP,则PD/PF=PB/BF

∵∠ADP=∠FPB,∠A=PBF,△ADP∽△BPF

∴PD/PF=AP/BF

∴PB/BF=AP/BF

∵PB=AP,PB/AP=1/2时,△PFD∽△BFP

其他回答

假设是反证法？？

其他类似问题

问题1：如图，点P是正方形ABCD边AB上一点（不与点A，B重合），连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F，连接BE，DF． （1）求证：∠ADP=∠EPB；（2）求∠CBE的度数；（3）当[数学科目]

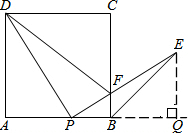（1）证明：∵四边形ABCD是正方形．
∴∠A=∠PBC=90°，AB=AD，
∴∠ADP+∠APD=90°，
∵∠DPE=90°，
∴∠APD+∠EPB=90°，
∴∠ADP=∠EPB；
（2） 过点E作EQ⊥AB交AB的延长线于点Q，则∠EQP=∠A=90°，
又∵∠ADP=∠EPB，PD=PE，
∴△PAD≌△EQP，
∴EQ=AP，AD=AB=PQ，
∴AP=EQ=BQ，
∴∠CBE=∠EBQ=45°；
（3） APAB

=12

．
理由：∵△PFD∽△BFP，
∴PBBF

=PDPF

∵∠ADP=∠EPB，∠CBP=∠A
∴△DAP∽△PBF
∴PDPF

=APBF

∴PA=PB
∴当APAB

=12

时，△PFD∽△BFP．

问题2：如图,以长为2的定线段AB为边作为正方形ABCD,取AB的中点P,连接PD,在BA的延具体见下方）急!如图,以长为2的定线段AB为边作为正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F使PF=PD,以AF为边作正[数学科目]

AB=2=AD,P为AB中点,则AP=1,

在Rt三角形APD中,利用勾股定理,AD^2+AP^2=PD^2,

代入数据计算得到PD=根号5=PF,所以AM=AF=PF-AP=(根号5)-1,

又AD=2,所以MD=AD-AM=3-(根号5);

所以AM/AD=(根号5-1)/2,

MD/AM=(3-根号5)/(根号5-1)=(根号5-1)/2,

AM/AD=MD/AM=(根号5-1)/2,

所以M是线段AD的黄金分割点.

(注)不好意思,我不会打"根号"这个符号,

问题3：点P是正方形ABCD边AB上一点（不与点A、B重合）,连接PD并将线段PD```如图,点P是正方形ABCD边AB上一点（不与点A、B重合）,连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE.[数学科目]

①证明:PE垂直PD,则∠EPB+∠APD=90°;

又∠ADP+∠APD=90°.

所以,∠ADP=∠EPB.

在AD上截取线段AQ=AP,连接PQ,则DQ=PB;∠AQP=∠APQ=45°,∠DQP=135°.

又PD=PE;∠ADP=∠EPB.故⊿DQP≌⊿PBE,∠PBE=∠DQP=135°,∠CBE=45°.

③当AQ=AP时,PQ=BE.

证明:AQ=AP时,DQ=PB;

又PD=PE;∠ADP=∠EPB.故⊿DQP≌⊿PBE,得PQ=BE.

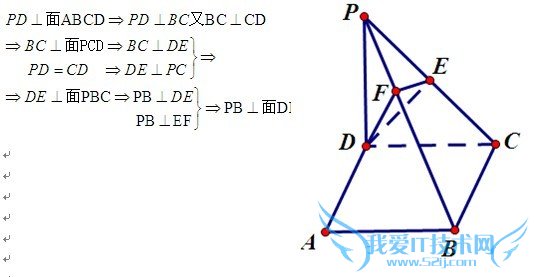
问题4：如图,PD垂直正方形ABCD所在的平面,PD=DC,E为PC的中点,EF垂直于PB于点F,求证,PB垂直于平面EFD[数学科目]

传统方法：如图

向量方法：建系D为原点,DA、DC、DP分别为x、y、z轴

目标：求点F的坐标,然后证明向量PB与向量DE、DF数量积均为零.

问题5：点P是正方形ABCD边AB上一点（不与A、B重合），连接PD并将线段PD绕点P顺时针旋转90°，得线段PE，连接BE，则∠CBE等于（　　） A. 75°B. 60°C. 45°D. 30°[数学科目]

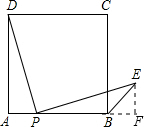过点E作EF⊥AF，交AB的延长线于点F，则∠F=90°，
∵四边形ABCD为正方形，
∴AD=AB，∠A=∠ABC=90°，
∴∠ADP+∠APD=90°，
由旋转可得：PD=PE，∠DPE=90°，
∴∠APD+∠EPF=90°，
∴∠ADP=∠EPF，
在△APD和△FEP中，
∵∠ADP＝∠FPE∠A＝∠F＝90°PD＝EP

，
∴△APD≌△FEP（AAS），
∴AP=EF，AD=PF，
又∵AD=AB，
∴PF=AB，即AP+PB=PB+BF，
∴AP=BF，
∴BF=EF，又∠F=90°，
∴△BEF为等腰直角三角形，
∴∠EBF=45°，又∠CBF=90°，
则∠CBE=45°．
故选C．