同学们提问关于“等腰三角形边长_已知△ABC为等腰三角形，由A点作BC边的高恰好等于BC边...[数学]”的问题，52IJ师说平台通过网络上精心整理了以下关于“等腰三角形边长_已知△ABC为等腰三角形，由A点作BC边的高恰好等于BC边...[数学]”的一些有用参考答案。请注意：文中所谈及的内容不代表本站的真正观点，也请不要相信各种联系方式。下面是本网所整理的“等腰三角形边长_已知△ABC为等腰三角形，由A点作BC边的高恰好等于BC边...[数学]”的相关信息：
已知△ABC为等腰三角形，由A点作BC边的高恰好等于BC边...
科目：数学 关键词：等腰三角形边长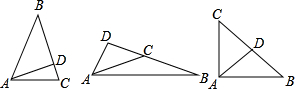
如下图，分三种情况：①AB=BC，AD⊥BC，AD在三角形的内部，
由题意知，AD=12
∵sin∠B=ADAB=12，
∴∠B=30°，∠C=180°?∠B2=75°，
∴∠BAC=∠C=75°；
②AC=BC，AD⊥BC，AD在三角形的外部，
由题意知，AD=12BC=12AC，
∵sin∠ACD=ADAC=12，
∴∠ACD=30°=∠B+∠CAB，
∵∠B=∠CAB，
∴∠BAC=15°；
③AC=BC，AD⊥BC，BC边为等腰三角形的底边，
由等腰三角形的底边上的高与底边上中线，顶角的平分线重合知，点D为BC的中点，
由题意知，AD=12BC=CD=BD，
∴△ABD，△ADC均为等腰直角三角形，
∴∠BAD=∠CAD=45°，
∴∠BAC=90°，
∴∠BAC的度数为90°或75°或15°，
故填90°或75°或15°．
其他类似问题
问题1：已知△ABC为等腰三角形，由A点作BC边的高恰好等于BC边长的一半，则∠BAC的度数为______．[数学科目]
如下图，分三种情况：①AB=BC，AD⊥BC，AD在三角形的内部，
由题意知，AD=12
∵sin∠B=ADAB=12，
∴∠B=30°，∠C=180°?∠B2=75°，
∴∠BAC=∠C=75°；
②AC=BC，AD⊥BC，AD在三角形的外部，
由题意知，AD=12BC=12AC，
∵sin∠ACD=ADAC=12，
∴∠ACD=30°=∠B+∠CAB，
∵∠B=∠CAB，
∴∠BAC=15°；
③AC=BC，AD⊥BC，BC边为等腰三角形的底边，
由等腰三角形的底边上的高与底边上中线，顶角的平分线重合知，点D为BC的中点，
由题意知，AD=12BC=CD=BD，
∴△ABD，△ADC均为等腰直角三角形，
∴∠BAD=∠CAD=45°，
∴∠BAC=90°，
∴∠BAC的度数为90°或75°或15°，
故填90°或75°或15°．
问题2：已知△ABC为等腰三角形，由A点作BC边的高恰好等于BC边长的一半，则∠BAC的度数为______．[数学科目]
如下图，分三种情况：①AB=BC，AD⊥BC，AD在三角形的内部，
由题意知，AD=12
∵sin∠B=ADAB=12，
∴∠B=30°，∠C=180°?∠B2=75°，
∴∠BAC=∠C=75°；
②AC=BC，AD⊥BC，AD在三角形的外部，
由题意知，AD=12BC=12AC，
∵sin∠ACD=ADAC=12，
∴∠ACD=30°=∠B+∠CAB，
∵∠B=∠CAB，
∴∠BAC=15°；
③AC=BC，AD⊥BC，BC边为等腰三角形的底边，
由等腰三角形的底边上的高与底边上中线，顶角的平分线重合知，点D为BC的中点，
由题意知，AD=12BC=CD=BD，
∴△ABD，△ADC均为等腰直角三角形，
∴∠BAD=∠CAD=45°，
∴∠BAC=90°，
∴∠BAC的度数为90°或75°或15°，
故填90°或75°或15°．
问题3：已知等腰△ABC，由顶点A所引BC边上的高线长等于BC边长的一半，求∠BAC的度数．[数学科目]
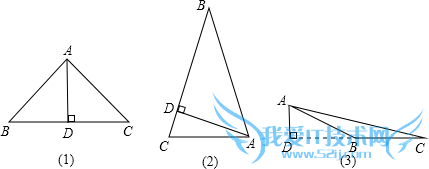
∵AD是BC边上的高线，
若BC是底边，即AB=AC，如图（1）所示，
∴BD=DC，AD⊥BC，∠BAD=∠CAD
∵AD=BD
∴∠B=∠BAD=45°
∴∠BAC=2∠BAD=90°
若BC是腰BC=BA，
①若点D在BC边上，如图（2）所示，
则在Rt△BAD中，
∵BA=2AD，
∴∠B=30°，
∴∠BAC=75°；
②若点D在CB的延长线上，如图（3）所示，
类似地，得：∠DBA=30°，
则：∠ABC=150°，
∴∠BAC=15°．
问题4：已知△ABC是等腰三角形,BC边上的高线长等于BC边长的一半,求∠BAC的度数,急啊!可以有过程么。。。一定要有过程啊[数学科目]
90°,因为三线（高线、底边的中线、顶角的平分线）合一,所以BC一定是底长,90°角啦
问题5：已知等腰△ABC，由顶点A所引BC边上的高线长等于BC边长的一半，求∠BAC的度数．[数学科目]
∵AD是BC边上的高线，
若BC是底边，即AB=AC，如图（1）所示，
∴BD=DC，AD⊥BC，∠BAD=∠CAD
∵AD=BD
∴∠B=∠BAD=45°
∴∠BAC=2∠BAD=90°
若BC是腰BC=BA，
①若点D在BC边上，如图（2）所示，
则在Rt△BAD中，
∵BA=2AD，
∴∠B=30°，
∴∠BAC=75°；
②若点D在CB的延长线上，如图（3）所示，
类似地，得：∠DBA=30°，
则：∠ABC=150°，
∴∠BAC=15°．
- 评论列表（网友评论仅供网友表达个人看法，并不表明本站同意其观点或证实其描述）
-