约瑟夫·拉格朗日_拉格朗日对数学的贡献有哪些﹖[历史]

精选知识

拉格朗日在数学上最突出的贡献是使数学分析与几何与力学脱离开来,使数学的独立性更为清楚,从此数学不再仅仅是其他学科的工具.

主要有以下四方面：

方程解法

在柏林工作的前十年,拉格朗日把大量时间花在代数方程和超越方程的解法上,作出了有价值的贡献,推动了代数学的发展.他提交给柏林科学院两篇著名的论文：《关于解数值方程》和《关于方程的代数解法的研究》.把前人解三、四次代数方程的各种解法,总结为一套标准方法,即把方程化拉格朗日点为低一次的方程(称辅助方程或预解式)以求解.

置换群

他试图寻找五次方程的预解函数,希望这个函数是低于五次的方程的解,但未获得成功.然而,他的思想已蕴含着置换群概念,对后来阿贝尔和伽罗华起到启发性作用,最终解决了高于四次的一般方程为何不能用代数方法求解的问题.因而也可以说拉格朗日是群论的先驱.

数论

在数论方面,拉格朗日也显示出非凡的才能.他对费马提出的许多问题作出了解答.如,一个正整数是不多于4个平方数的和的问题等等,他还证明了圆周率的无理性.这些研约瑟夫·拉格朗日点究成果丰富了数论的内容.

幂级数

在《解析函数论》以及他早在1772年的一篇论文中,在为微积分奠定理论基础方面作了独特的尝试,他企图把微分运算归结为代数运算,从而抛弃自牛顿以来一直令人困惑的无穷小量,并想由此出发建立全部分析学.但是由于他没有考虑到无穷级数的收敛性问题,他自以为摆脱了极限概念,其实只是回避了极限概念,并没有能达到他想使微积分代数化、严密化的目的.不过,他用幂级数表示函数的处理方法对分析学的发展产生了影响,成为实变函数论的起点.

其他类似问题

问题1：拉格朗日中值定理对数学的贡献

微分学的基础,该定理又叫微分中值定理,可见它在微分学中的地位.

问题2：数学微积分（拉格朗日中值定理问题）2、3

问题3：拉格朗日中值定理的应用

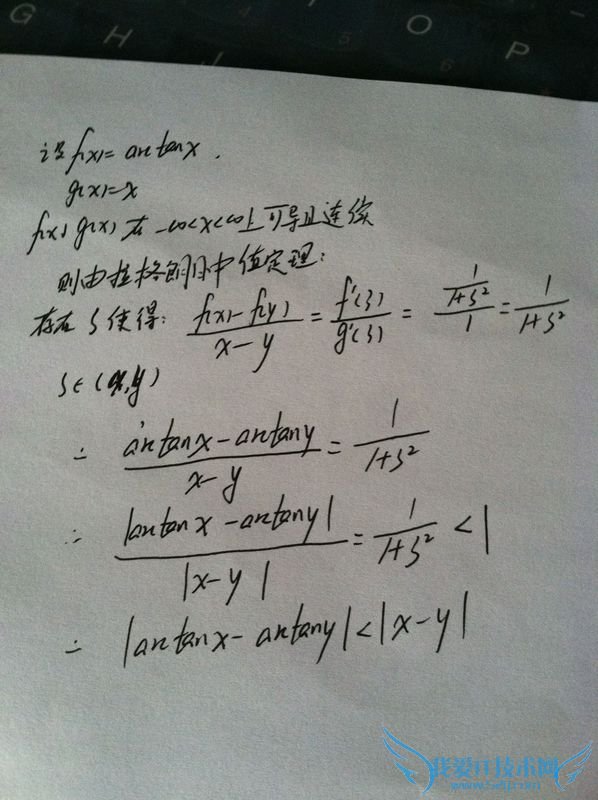
问题4：式子是这样的 lnx+y+aln(5-x)- 入（px*x+py*y-5px) ,要求分别对X Y 入三个变量求导令为0,解出X和Y,X和Y的表达式里只能有px ,py ,a 这三个常数（px py就是x y的价格,是常数）考试怎么也算不出来.[数学科目]

f(x,y,入)=lnx+y+aln(5-x)- 入（px*x+py*y-5px),对x,y,入分别求偏导数并令为0得到以下方程组:

1/x-a/(5-x)+入px=0

1+入py=0

px*x+py*y-5px=0

解方程得到X=py*(a+1)/(2px) +/- py*Sqrt[(a+1)^2-20px/py]/(2px), Y=5px/py +(a+1)/2 +/- Sqrt[(a+1)^2-20px/py]/2

纯手工算出,望采纳,欢迎追问,谢谢!

问题5：拉格朗日 09年这两个分别是代表什么意义,不都是 导函数在零点的右极限 不是天然相等吗?还需要证明什么.[数学科目]

已知：f(x) 在 (0,δ) 可导,且 f(x) 的导函数在零点的右极限 = A,

求证：f(x) 在零点的右导数 = A.

注意：已知条件中没有说 f(x) 在零点可导,只说在 (0,δ) 可导,现在要求证明 f(x) 在零点的右导数存在.