一次函数_已知一次函数y=？12x+4的图象与x轴、y轴分别相交于...[数学]

精选知识

（1）∵一次函数y＝?12x+4

的图象与x轴、y轴分别相交于点A、B，
∴A（8，0），B（0，4）．
在梯形AOBC中，OA=8，OB=4，AC=5，
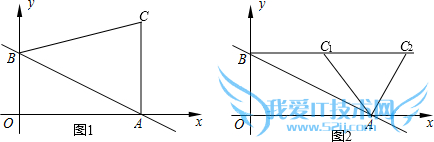
当AC∥OB时（如图1），点C的坐标为（8，5），
当BC∥OA时（如图2），设点C（x，4）．
∵AC=5，
∴（x-8）²+（4-0）²=5²，
∴x₁=5，x₂=11，
这时点C的坐标为（5，4）或（11，4），
∴点C的坐标为（8，5）或（5，4）或（11，4）；

（2）∵点A、C在一次函数y=kx+b（k＜0）的图象上，
∴点（8，5）与（11，4）都不符合题意，只有当C为（5，4）时，k＜0，
∴0＝8k+b4＝5k+b

，
∴k＝?43b＝323.

，
∴这个一次函数的解析式为y＝?43x+323

．

其他回答

用函数可算A，B坐标

再用两点间距离公式

可算C

A，C知道了，带入y=kx+b，算出kb，注意k<0

其他类似问题

问题1：已知一次函数y=1/2+4的图像与x轴、y轴非别叫于点A,B点,梯形AOBC的边AC为5,求点C坐标似乎有三个解[数学科目]

y=1/2*x+4?

A(-8,0),B(0,4)

AC是边所以AO,BC是底

是直角梯形

所以只有两个解（-5,4）和（-11,4）

你当3个解可能是把AC作为底了这样算（-8,5）也是一个解

问题2：已知一次函数y=½x+4的图像与x轴、y轴分别交于点A、B,梯形AOBC（O是原点）的边AC=5,求C点的坐标点A交于X轴,点B交于Y轴,[数学科目]

y=0时,x=8 所以A(8,0)

x=0时,y=4所以B（0,4）

梯形AOBC,所以c点x坐标为8或者y坐标为4

c点x坐标为8时,AC=5所以c点y坐标为5;C(8,5)

c点y坐标为4时,AC=5所以5^2=4^2+(8-x)^2 c点x坐标为 5或者11

问题3：已知一次函数y=-2/1x+4的图像与x轴、y轴分别相交于点A、B.梯形AOBC的边AC=5,且0A平行于BC.（1）求点C的坐标；（2）如果点A、C在一次函数y=kx+b（k、b为常数,且k＜0）的图像上,求这个一次函数的解[数学科目]

A(2,0),B(0,4),C(5,4)（这不用画图了吧）

k=（4-0）/（5-2）=4/3,

把A点代入 得 b=0-2*k=-8/3,

得y=4/3*x-8/3.

问题4：已知一次函数y=-1/2x+4的图像与x轴,y轴分别相交于点A.B,四边形AOBC(O是原点）的一组对边平行,边AC=5.(连接上面）（1）求点c的坐标；（2）如果一个一次函数y=kx+b(k.b为常数,且k[数学科目]

⑴令X=0,Y=4,令Y=0,X=8,

∴A(8,0),B(0,4),

①当AC∥OB,且AC=5,则C1(8,5),C2(8,-5),

②当BC∥OA,则C3(5,4),C4(11,4).

⑵直线过C1、C2时,K不存在,与K

问题5：已知一次函数y＝?12x+4的图象与x轴、y轴分别相交于点A、B．梯形AOBC的边AC=5．（1）求点C的坐标；（2）如果点A、C在一次函数y=kx+b（k、b为常数，且k＜0）的图象上，求这个一次函数的解析式[数学科目]

（1）∵一次函数y＝?12x+4

的图象与x轴、y轴分别相交于点A、B，
∴A（8，0），B（0，4）．
在梯形AOBC中，OA=8，OB=4，AC=5，
当AC∥OB时（如图1），点C的坐标为（8，5），
当BC∥OA时（如图2），设点C（x，4）．
∵AC=5，
∴（x-8）²+（4-0）²=5²，
∴x₁=5，x₂=11，
这时点C的坐标为（5，4）或（11，4），
∴点C的坐标为（8，5）或（5，4）或（11，4）；

（2）∵点A、C在一次函数y=kx+b（k＜0）的图象上，
∴点（8，5）与（11，4）都不符合题意，只有当C为（5，4）时，k＜0，
∴0＝8k+b4＝5k+b

，
∴k＝?43b＝323.

，
∴这个一次函数的解析式为y＝?43x+323

．