欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“xxixi_...x+2与曲线xIxIm+yIyIn=1交点个数为 个.238.15....[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
由均值不等式
1=1/m+2/n≥2根号(1/m*2/n)
当且仅当1/m=2/n时等号成立
也就是1/m=2/n=0.5
所以m=2 n=4
所以xIxI/m+yIyI/n=1
为xIxI/2+yIyI/4=1
讨论
①当x>0 y>0
表示x²/2+y²/4=1的椭圆
②当x>0 y<0
表示x²/2-y²/4=1以x轴为实轴的双曲线
③当x<0 y>0
表示y²/4-x²/2=1以y轴为实轴的双曲线
④当x<0 y<0
表示-x²/2-y²/4=1
因为左边恒≤0所以不可能=右边
所以此时无解
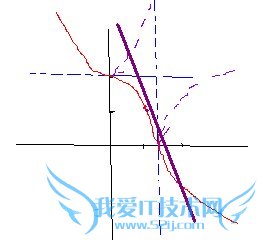
所以如图得到图像(红色部分)
有点粗的那条是y=-根号2+2的直线
与图像相交正好有两个交点(1/4个椭圆一个 与下面的双曲线部分一个)
注意:与x>0 y>0表示x²/2+y²/4=1的椭圆相交的时候正好相切
你把直线代入 可以求得(根号2x-1)²=0 得到为(根号2/2,1)
其他回答
很常用的a+b定值时,且A,B均大于0,那a=b时,就是ab取最大值(a+b)^2/4
看这道题,就成了,1/m=2/n时,2/mn取最大值,也就是mn取最小值啦
做题就记住方法,这个知识点常用的
其他类似问题
问题1:M,N是曲线y=πsinx与曲线y=πcosx的两个不同的交点,则|MN|的最小值为( )A. πB. 2πC. 3πD. 2π[数学科目]
要求|MN|的最小值在,只要在一个周期内解即可
∵πsinx=πcosx 解得x=π 4
| 5π |
| 4 |
得到两个点为(,
| π |
| 4 |
| ||
| 2 |
| 5π |
| 4 |
| ||
| 2 |
得到|MN|=
(
(?
|
| 3 |
故选C
问题2:已知点M,N是曲线y=sinπx与曲线y=cosπx的两个不同的交点,则|MN|的最小值为?[数学科目]
sinπx=cosπx
sinπx-cosπx=0
√2(√2/2*sinπx-√2/2cosπx)=0
√2sin(πx-π/4)=0
πx-π/4=kπ
取相邻的两个k值,如k=0和k=1,得:
x1=1/4,x2=5/4
代入原曲线,得:
y1=sin(π/4)=√2/2,y2=sin(5π/4)=-√2/2
即为相邻两交点M(x1,y1)、N(x2,y2)
|MN|=√[(x1-x2)^2+(y1-y2)^2]=√3
问题3:M是抛物线y^2=x上一点,N是圆(x+1)^2+(y-4)^2=1关于直线x-y+1=0的对称曲线上一点.求MN的最小值.[数学科目]
直线 x-y+1=0可改写为y=x+1或x=y-1,
所以,圆(x+1)^2+(y-4)^2=1关于直线x-y+1=0的对称曲线为圆 (x-3)^2+y^2=1,
其圆心为 P(3,0),半径为 1.
设M(y^2,y)是抛物线 y^2=x上任一点,
则 |MP|^2=(y^2-3)^2+y^2=y^4-5y^2+9=(y^2-5/2)^2+11/4,
所以,当 y^2=5/2时,|MP|最小值为 √11/2.
又由于 √11/2>1,
因此,MN的最小值为 √11/2-1=(√11-2)/2.
问题4:已知1/m+2/n=1(m>0,n>0),则mn的最小值是[数学科目]
最小值为8.
因为m+n>=2√mn,m+2n>=2√2mn
由1/m+2/n=1可得2m+n=mn
然后两个式子一结合就出来了
具体对不对不清楚,好久没看过不等式的高中内容
问题5:已知2m+n=1,其中m,n均为正数,则1m+2n的最小值为( )A. 2B. 4C. 8D. 16[数学科目]
∵2m+n=1,其中m,n均为正数,
∴1 m
| 2 |
| n |
| 1 |
| m |
| 2 |
| n |
| n |
| m |
| 4m |
| n |
|
| 1 |
| 2 |
故选:C.
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
