欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“cf云影_...BC=2AD,点f在bc延长线上,AF与BD交于点E,AD=2CF,求...[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
是16/7
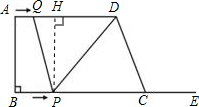
过G作GH//DF交BC于H
CG/DG=CF/AD=1/2 CG=1/2DG=1/3CD
CH/BC=CG/CD=1/3 CH=1/3BC=2/3AD FH=CF+CH=(2/3+1/2)AD=7/6AD
BF=(2+1/2)AD=5/2AD BH=BC-CH=4/3AD
FG/EG=FH/BH=7/6AD/(4/3AD)=7/8
Sfcg/Sdge=FG*GC/(DG*EG)=1/2*7/8=7/16 对顶角正弦相等
Sdge/Sfcg=1/(7/16)=16/7
其他类似问题
问题1:如图,在梯形ABCD中,AD‖CB,AD=2,BC=8,AC=6,BD=8,求梯形ABCD的面积.[数学科目]
平移AC,使A与D重合,C平移到了C‘ 此时AC’的平方+BD的平方=BC'的平方 所以AC'⊥BD,所以AC⊥BD 梯型面积就等于AC×BD×½=24
问题2:如图,在梯形ABCD中,AD∥BC,AB=AD=DC,AC⊥AB,延长CB至F,使BF=CD. (1)求∠ABC的度数;(2)求证:△CAF为等腰三角形.[数学科目]
(1)∵AD∥BC,
∴∠DAC=∠ACB.
∵AD=DC,
∴∠DCA=∠DAC.
∴∠DCA=∠ACB=1 2
∵DC=AB,
∴∠DCB=∠ABC.
∴∠ACB=
| 1 |
| 2 |
在△ACB中,∵AC⊥AB,
∴∠CAB=90°.
∴∠ACB+∠ABC=90°.
∴
| 1 |
| 2 |
∴∠ABC=60°.(3分)
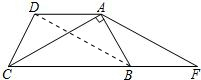 (2)证明:连接DB,
(2)证明:连接DB,∵在梯形ABCD中,AB=DC,
∴AC=DB.
在四边形DBFA中,DA∥BF,DA=DC=BF,
∴四边形DBFA是平行四边形.
∴DB=AF,
∴AC=AF.
即△ACF为等腰三角形.(6分)
问题3:已知如图在梯形abcd中,AD∥BC,延长CB到点E,使BE=AD.连结DE,交AB与点M[数学科目]
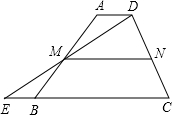
(1)证明:∵AD∥BC,
∴∠A=∠MBE,∠ADM=∠E,
在△AMD和△BME中,
∠A=∠MBE
AD=BE
∠ADM=∠E
∴△AMD≌△BME(ASA);
(2)∵△AMD≌△BME,
∴MD=ME,ND=NC,
∴MN= 1/2EC
∴EC=2MN=2×5=10,
∴BC=EC-EB=10-2=8.
答:BC的长是8.
问题4:如图,在梯形ABCD中,AB平行DC,AD=DC=CB=3,DB⊥AD,求∠A的度数及梯形的周长 连接BDD _______C/ \/__________\BA[数学科目]
连接BD,AB平行DC,
所以∠CDB=∠DBA,
又因为AD=DC=CB=3,
所以△CDB是等腰三角形,有∠CBD=∠CDB=∠DBA,
又因为梯形ABCD是等腰梯形
所以∠DAB=∠CBA,∠DAB=2=∠DBA
又因为DB⊥AD,所以∠BDA=90°
所以在三角形ADB中
∠DAB+∠DBA+90°=180°即3∠DBA=90°,∠DBA=30°
所以∠DAB=60°即∠A=60°
所以AB=2AD=6
梯形ABCD的周长=3+3+3+6=15
问题5:附加题 (1)试用一元二次方程的求根公式,探索方程ax+bx+c=0(a≠0)的两根互为倒数的条件是______;(2)如图.边长为2的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针[数学科目]
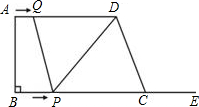
(1)若方程两根互为倒数则两根之积为1,故a=c;
(2)根据旋转的性质,两个正方形重叠部分的面积为三角形ABE面积的2倍,
由题意可知,BE=22
| 2 |
故两个正方形重叠部分的面积为4
| 2 |
(3)①∵四边形PQDC是平行四边形,
∴DQ=CP,
∵DQ=AD-AQ=16-t,CP=21-2t,
∴16-t=21-2t,
解得t=5,
当t=5秒时,四边形PQDC是平行四边形,
②若点P,Q在BC,AD上时,
| DQ+CP |
| 2 |
| 16?t+21?2t |
| 2 |
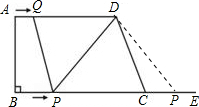
解得t=9(秒),
若点P在BC延长线上时,则CP=2t-21,
∴
| 2t?21+16?t |
| 2 |
解得t=15(秒),
∴当t=9或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2;
③当PQ=PD时,
作PH⊥AD于H,则HQ=HD,
∵QH=HD=
| 1 |
| 2 |
| 1 |
| 2 |
由AH=BP得2t=
| 1 |
| 2 |
解得t=
| 16 |
| 3 |
当PQ=QD时QH=AH-AQ=BP-AQ=2t-t=t,QD=16-t,
∵QD2=PQ2=122+t2,
∴(16-t)2=122+t2解得t=
| 7 |
| 2 |
当QD=PD时DH=AD-AH=AD-BP=16-2t,
∵QD2=PD2=PH2+HD2=122+(16-2t)2,
∴(16-t)2=122+(16-2t)2,
即3t2-32t+144=0,
∵△<0,
∴方程无实根,
综上可知,当t=
| 16 |
| 3 |
| 7 |
| 2 |
- 75xy.com_...x 2 y}+[- 1 4 xy 2 +(- 3 16 x 2 y-
- 6.1儿童节短信_开放题:六一儿童节那天,六(3)班
- 丶_丶如题、、、如图,D为线段AF上一点,AD=a,DF
- 是不是_A∩A是否=A[数学]
- baidu.c om_...点a b在oq上 ob=ab ac⊥on于点c p
- 不患无位 患所以立_不患无位患所以立后面是哪几句
- 60abc_如图,△ABC中,∠ABC=60°,AD、CE分别平
- 2011深圳中考数学_...1,则正切A是多少?也就是深
- 唇亡齿寒的近义词_唇亡齿寒的近义词是什么?所以.
- 已知a b互为相反数_已知2-b与a-b+4互为相反数,求
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
