y=f(g(x))的二阶导数怎么求

精选知识

y'=f‘ （g（x））g’（x）

y''=(y')'=(f‘ （g（x））g’（x）)'=(f''(g(x))g'(x))*g’（x）+f‘(g（x))*g''(x)=f''(g(x))[g'(x)]^2+f‘(g（x))*g''(x)

其他类似问题

问题1：已知f(x)与g(x)可导,且f(x)^2+g(x)^2不等于0,求y=[f(x)^2+g(x)^2]^(1/2)的导数.{^2为平方,^(1/2)为开根号.[数学科目]

复合函数求导采用的是层层剥的方法,解法如下(那个y的代数式太复杂了,我就不写全了,直接用y代替好了)

y'=1/2*1/y*[2f(x)f'(x)+2g(x)g'(x)]

问题2：设g(r)有一阶导数,f(x,y)=g(r),r=√(x^2+y^2).求?f/?y,?f/?x[数学科目]

?f/?y=g'(r)2y /根号下(x^2+y^2)

?f/?x=g'(r)2x/根号下(x^2+y^2)

问题3：设u=f[g(x)+y^2],其中y=y(x)由方程y十e^y=xf(x)确定,g(x)有一阶导数,求d(u)/d(x)[数学科目]

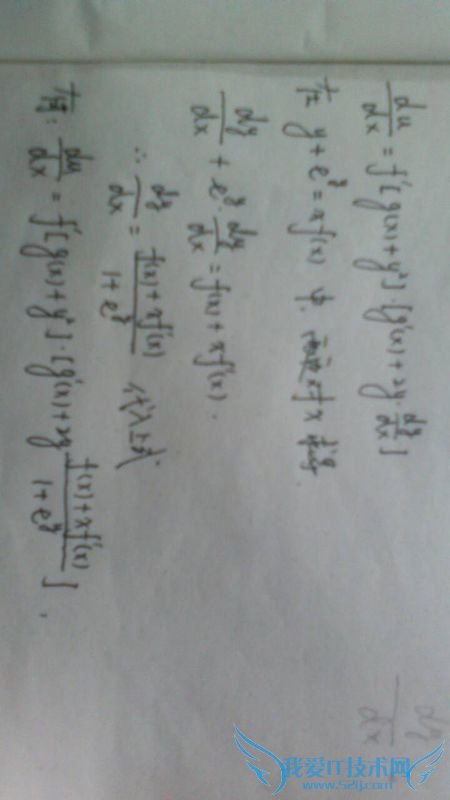
问题4：设F(x,y)=f(x)g(y),其中f,g为导数连续的一元函数,1.如果存在导数连续的 一元函数s(r)使得F(rcosθ,rsinθ)=s(r),求F(x,y)2.如果存在导数连续的 一元函数使得F(rcosθ,rsinθ)=φ(θ),求F(x,y)[数学科目]

令x = rcosθ,

y = rsinθ

所以x^2+y^2 = r^2

r = √(x^2+y^2)

所以F(x,y) = s(r) = s(√(x^2+y^2))

同理

tanθ = y/x

F(x,y) = φ(arctan(y/x))

问题5：y = [ f(x) + 2 ] / g(x),则y的导数为?怎么求的,看起来好复杂啊,[数学科目]

y'={[f(x)＋2]'g(x)－g'(x)[f(x)＋2]}/[g2(x)]

={f'(x)g(x)－g'(x)[f(x)＋2]}/[g2(x)]