2元1次方程求根公式

精选知识

二元一次方程：ax^2+bx+c=0 (a不等于0）

求根公式是：x1=[-b+根号下（b^2-4ac)]/2ab

x2=[-b-根号下（b^2-4ac)]/2ab

其他回答

x=[-b±√(b^2-4ac)]/(2a)

其他类似问题

问题1：二元一次不定方程求根公式是怎么样的?37x+89y=999,已知其中一个解为:X1=-62,Y1=37,求这个不定方程的通式,好象高中的时候学过,现在全忘了.[数学科目]

不定方程ax+by=c,(a,b)=1,若（x0,y0)是一组解,则所有解可表成：

x=x0+bt

y=y0-at,（t是整数)

下面证明一下

为表示方便,设x1=x0+bt,y1=y0-at是任一组解

一方面,把x1,x2表达式代入ax+by=a(x0+bt)+b(y0-at)

=ax0+abt+by0-abt=ax0+by0=c

所以(x1,y1)确是ax+by=c的解,且(x1,y1)=(x0,y0)只要取t=0即可

另一方面,设ax+by=c有另一组解(x1,y1),则有方程组

ax0+by0=c①

ax1+by1=c②

①-②得a(x1-x0)=b(y0-y1)

根据整除性质,显然有a│b(y0-y1),b│a(x1-x0)

但(a,b)=1故有a│y0-y1,b│x1-x0

不妨设x1-x0=bt1,y0-y1=at2(t1,t2∈Z),则x1=x0+bt1,y1=y0-at2,

代入②得a(x0+bt1)+b(y0-at2)=c+ab(t1-t2)=c

故ab(t1-t2)=0,所以t1=t2

设t1=t2=t,则通解为x=x0+bt,y=y0-at

证毕!

问题2：知道的请告诉一下二元2次方程求根公式,[数学科目]

转化成一元二次方程

用求根公式解

问题3：二元一次方程求根公式是[数学科目]

x=[－b±根号﹙b2－4ac﹚]／﹙2a﹚

b2－4ac≥0

问题4：求解二元方程根公式谢谢!急啊[数学科目]

2a/b^2一或+根号b^2一4ac

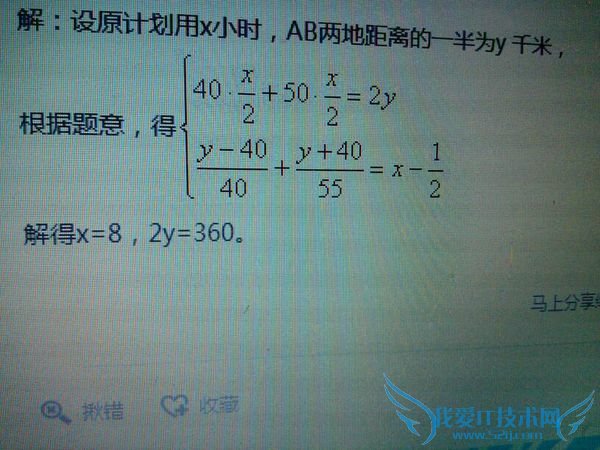
问题5：二元一次的方程方法求解 [数学科目]