如图，A，C两点在直线L上，AC=6，D为射线CM上一点，CD=7，...

精选知识

因为QA=2QC,所以求2QD+QA的最小值就是求2QD+2QC的最小值.

QD+QC≥CD,所以QD+QC最小值为CD=7,题中所求最小值为14

其他回答

找《重点难点》，里面应该有。

其他类似问题

问题1：如图，为了确定一条经过点D且与直线AB平行的直线，小明同学在直线AB上取一点C，在直线AB外取一点E，恰好量得∠2=80°，∠D=50°，∠1=∠3，这时，小明说AB与DE平行了，他说得对吗？为什么？[数学科目]

对．
∵∠2=80°，∠1=∠3，
∴2∠1+∠2=180°，
∴∠1=∠3=50°；
∵∠D=50°，
∴∠1=∠D=50°，
∴AB∥DE．

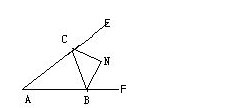
问题2：已知在△ABC中,∠A=40° （1）如图①,角平分线BM和CM交于点M,求∠BMC的度数（2）如图②,外角平分线BN和CN交于点N,求∠BNC的度数.[数学科目]

1 解 ∵∠A=40°

∴∠ABC+∠ACB=140°

又∵BM,CM分别平分∠ABC、∠ACB

　 ∴∠BCM+∠CBM=1/2（∠ABC＋∠ACB)=1/2×140°=70°

∴∠BMC=180°-70°=110°

2 解 ∵∠A=40°

∴∠ACB+∠ABC=140°

∴∠ECB+∠CBF=360°-140°=220°

又∵BN,CN分别平分∠CBF、∠ECB

∴ ∠BCN+∠CBN=1/2(∠ECB+∠CBF)=1/2×220°=110°

∴BNC=180°-(∠BCN+∠CBN)=180°-110°=70°

(2)

问题3：在△ABC中，∠C=2∠B，∠1=∠2，试说明AB=AC+CD．[数学科目]

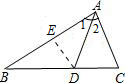证明：在AB上取一点E使AE=AC，
∵∠1=∠2，AE=AC，AD=AD，
∴△ADC≌△ADE．
∴DE=DC，∠AED=∠C．
∵∠AED=∠B+∠EDB，∠C=2∠B，
∴∠B=∠EDB．∴BE=DE．
又∵DE=DC，
∴BE=DC．
∵AB=AE+BE，
∴AB=AC+DC．

问题4：如图1是一个三角形金属轨道△ABC,其周长132cm,AB=AC.P,Q,R三个小球如图1是一个三角形金属轨道△ABC,其周长132cm,AB=AC.P,Q,R三个小球分别从A,B,C出发以相同的速度向B,C,A运动.当运动了6秒,有AP=四分之[数学科目]

1

设速度X

则AP=BQ=6X,AB=24X=AC,BC=18X

24X*2+18X=132

X=2

AB=AC=48,BC=36

2

BC边最短

则Q与R首次同时在AC上,同时的时间=（48-36）/2=6秒

3

设时间X

36-2X=6X

X=4.5

问题5：如图，数轴上A，B两点表示的数分别为-2和6，数轴上的点C满足AC=BC，点D在线段AC的延长线上，若AD＝32AC，则BD=______，点D表示的数为______．[数学科目]

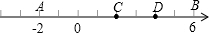∵A，B两点表示的数分别为-2和6，
∴AB=6-（-2）=8，
∵AC=BC=12

AB=12

×8=4，
∵AD=32

AC=32

×4=6，
∴OD=AD-AC=6-2=4，
∴BD=6-4=2，
点D表示的数是4．
故答案为：2；4．