...该城市一年被塑料袋污染的土地是多少？(保留2个有...

精选知识

拜托,是100万,还是100百万啊?当是100万.

(1) 1000000*365=3.65*10^8(个)~3.7*10^8

(2) 3.7*10^8/1000=3.7*10^5(平方米)

答：.

其他回答

1000000*1*365=365000000

365000000/1000*1=36500

其他类似问题

问题1：已知abc=1,不改变分式的值,使分式1/ab+b+1,1/bc+c+1的分母与1/ca+a+1的分母相同.[数学科目]

1/(ab+b+1)

=abc/(ab+b+abc)

=ac/(ac+a+1)

1/(bc+c+1)

=abc/(bc+c+abc)

=ab/(ab+b+1)

=ab/(ab+b+abc)

=a/(ac+a+1)

1/(ca+a+1)

=1/(ac+a+1)

此时三个分式分母相同.

问题2：初中数学,怎么根号化简?【1】请简单点说明方法,【2】然后我举几个例子,例如√12怎么化简?3√5怎么化简?[数学科目]

这个很基础的哟,你把根化里的数化成单个单个相乘的,把偶数个的提取出来.

如√12可以化成√2*2*3,其中2是偶数个,提一个出来,结果是2√3,

再如3√5往里化,相反,结果是√3*3*5=√45.懂了吗,不懂再问,记得给分!

问题3：一道初中数学题如图所示

因为

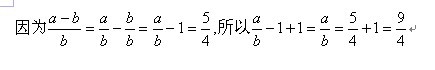
问题4：初中数学论文怎么写?急![历史科目]

黄金分割

对于“黄金分割”大家应该都不陌生吧!

由于公元前6世纪古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,因此现代数学家们推断当时毕达哥拉斯学派已经触及甚至掌握了黄金分割. 公元前4世纪,古希腊数学家欧多克索斯第一个系统研究了这一问题,并建立起比例理论.

公元前300年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果,进一步系统论述了黄金分割,成为最早的有关黄金分割的论著. 中世纪后,黄金分割被披上神秘的外衣,意大利数家帕乔利称中末比为神圣比例,并专门为此著书立说.德国天文学家开普勒称黄金分割为神圣分割. 到19世纪黄金分割这一名称才逐渐通行.黄金分割数有许多有趣的性质,人类对它的实际应用也很广泛.最著名的例子是优选学中的黄金分割法或0.618法,是由美国数学家基弗于1953年首先提出的,70年代在中国推广.

也许,0.618在科学艺术上的表现我们已了解了很多,但是,你有没有听说过,0.618还与炮火连天、硝烟弥漫、血肉横飞的惨烈、残酷的战场也有着不解之缘,在军事上也显示出它巨大而神秘的力量?一代枭雄的的拿破仑大帝可能怎么也不会想到,他的命运会与0.618紧紧地联系在一起.1812年6月,正是莫斯科一年中气候最为凉爽宜人的夏季,在未能消灭俄军有生力量的博罗金诺战役后,拿破仑于此时率领着他的大军进入了莫斯科.这时的他可是踌躇满志、不可一世.他并未意识到,天才和运气此时也正从他身上一点点地消失,他一生事业的顶峰和转折点正在同时到来.后来,法军便在大雪纷扬、寒风呼啸中灰溜溜地撤离了莫斯科.三个月的胜利进军加上两个月的盛极而衰,从时间轴上看,法兰西皇帝透过熊熊烈焰俯瞰莫斯科城时,脚下正好就踩着黄金分割线.

古希腊帕提侬神庙是举世闻名的完美建筑,它的高和宽的比是0.618.建筑师们发现,按这样的比例来设计殿堂,殿堂更加雄伟、美丽；去设计别墅,别墅将更加舒适、漂亮．连一扇门窗若设计为黄金矩形都会显得更加协调和令人赏心悦目．

有趣的是,这个数字在自然界和人们生活中到处可见：人们的肚脐是人体总长的黄金分割点,人的膝盖是肚脐到脚跟的黄金分割点.大多数门窗的宽长之比也是0.618…；有些植茎上,两张相邻叶柄的夹角是137度28',这恰好是把圆周分成1:0.618……的两条半径的夹角.据研究发现,这种角度对植物通风和采光效果最佳.黄金分割与人的关系相当密切.地球表面的纬度范围是0——90°,对其进行黄金分割,则34.38°——55.62°正是地球的黄金地带.无论从平均气温、年日照时数、年降水量、相对湿度等方面都是具备适于人类生活的最佳地区.说来也巧,这一地区几乎囊括了世界上所有的发达国家.

多去观察生活,你就会发现生活中奇妙的数学!

数字

中国有一个成语——“顾名思义”.很多事物都能顾名思义,但是也有例外.比如,阿拉伯数字.很多人一听到阿拉伯数字,就会认为是阿拉伯人发明的.但事实证明,不是. 阿拉伯数字1、2、3、4、5、6、7、8、9.0是国际上通用的数码.这种数字的创制并非阿拉伯人,但也不能抹掉阿拉伯人的功劳.其实,阿拉伯数字最初出自印度人之手,是他们的祖先在生产实践中逐步创造出来的.

公元前3000年,印度河流域居民的数字就已经比较进步,并采用了十进位制的计算法.到吠陀时代（公元前1400－公元前543年）,雅利安人已意识到数码在生产活动和日常生活中的作用,创造了一些简单的、不完全的数字.公元前3世纪,印度出现了整套的数字,但各地的写法不一,其中典型的是婆罗门式,它的独到之处就是从1～9每个数都有专用符号,现代数字就是从它们中脱胎而来的.当时,“0”还没有出现.到了笈多时代（300－500年）才有了“0”,叫“舜若”（shunya）,表示方式是一个黑点“●”,后来衍变成“0”.这样,一套完整的数字便产生了.这就是古代印度人民对世界文化的巨大贡献.

印度数字首先传到斯里兰卡、缅甸、柬埔寨等国.7－8世纪,随着地跨亚、非、欧三洲的阿拉伯帝国的崛起,阿拉伯人如饥似渴地吸取古希腊、罗马、印度等国的先进文化,大量翻译其科学著作.771年,印度天文学家、旅行家毛卡访问阿拉伯帝国阿拨斯王朝（750－1258年）的首都巴格达,将随身携带的一部印度天文学著作《西德罕塔》献给了当时的哈里发曼苏尔（757－775）,曼苏尔令翻译成阿拉伯文,取名为《信德欣德》.此书中有大量的数字,因此称“印度数字”,原意即为“从印度来的”.

阿拉伯数学家花拉子密（约780－850）和海伯什等首先接受了印度数字,并在天文表中运用.他们放弃了自己的28个字母,在实践中加以修改完善,并毫无保留地把它介绍给西方.9世纪初,花拉子密发表《印度计数算法》,阐述了印度数字及应用方法.

印度数字取代了冗长笨拙的罗马数字,在欧洲传播,遭到一些基督教徒的反对,但实践证明优于罗马数字.1202年意大利雷俄那多所发行的《计算之书》,标志着欧洲使用印度数字的开始.该书共15章,开章说：“印度九个数字是：‘9、8、7、6、5、4、3、2、1’,用这九个数字及阿拉伯人称作sifr（零）的记号‘0’,任何数都可以表示出来.”

14世纪时中国的印刷术传到欧洲,更加速了印度数字在欧洲的推广应用,逐渐为欧洲人所采用.

西方人接受了经阿拉伯人传来的印度数字,但忘却了其创始祖,称之为阿拉伯数字.

问题5：初中数学小论文：数学中的乐趣[政治科目]

小议数学教学中的乐趣

在中学数学教学中,应积极进行愉快教学,以培养学生学习数学的兴趣,从而激发学生高效率地学习数学.所谓愉快教学,是指在教学过程中,充分发挥教师和学生两方面的积极性,教师乐教,学生乐学.在轻松愉快、情绪饱满、没有精神压力、没有心理负担的状态下,大脑皮层容易形成兴奋中心,激活神经系统,从而取得良好的教学效果.因此,实施愉快教学是学生身心健康发展的需要,是提高学习质量和教学质量的需要,也是学校减轻学生负担,实施素质教育的需要.国内外大量的心理学、教育学研究结果表明：学生学习成绩的好坏,并不完全取决于智力水平的高低,非智力因素如学习目的、学习兴趣、爱好、情感、意志力等直接影响到一个人整体心理素质水平和事业的成败.非智力因素的发展所激发的潜能在某种程度上可以弥补智力因素方面的不足,同时对智力因素的发展起到积极的推动作用.初中阶段的学生正处于青春发育期,除生理方面产生较大的变化外,心理方面的变化更会对其成长过程产生不可忽视的影响.初中数学教师在其教学中应利用情感、兴趣、需要等非智力因素激发学生的求知欲,诱导学生乐学、爱学,变“要我学”为“我要学”,让学生在愉快和谐的情感氛围中轻松地学习,最终达到教学效率、教学质量全面提高,推动数学素质教育全面发展的目的.

数学是人们生活、劳动和学习必不可少的工具,数学知识无处不在.作为一名中学数学教师,应该拥有一双“慧眼”,应善于从生活中、周围环境中、各种媒体中捕捉数学知识,从小处、平常处着眼,从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型,并进行解释与应用的过程.通过联系实际、因势利导、循循善诱,结合一些新的教学辅助手段,培养起学生对数学知识的浓厚兴趣,使学生感到学习数学知识是件愉快的事情.

一、建立融洽和谐的师生关系

和谐融洽的师生关系是实施愉快教学的前提和基础,也是诸多人际关系中的主导因素.师生关系好,学生爱老师,就会“爱屋及乌”,爱其所教的学科；师生关系好,学生对老师的信任度高,就会产生“亲其师,信其道”的效应,教师教给的各种信息就会在学生头脑里出现一种“易接受”的心理优势；师生关系好,学生的崇拜度高,教师的模范言行、治学精神都给学生以感染.在教学中教师应尊重学生人格,尊重学生的主体地位和创新精神,平等公正地对待每个学生,同时,教学中教师亲切和蔼的表情、幽默有趣的话语都会给学生带来良好的心境和强烈的求知欲,自觉实现教学过程中默契配合的最优化.

二、充分满足学生的基本需要

人的认知需要、成就需要是人的较高层次的需要,是一种成长性的需要.一般来说,高层次的、成长性的需要的充分表现有赖于低层次需要的大致满足.有生存才有发展,“衣食足而知礼仪”.要激发学生的高层次的求知欲望,就应注意尽量满足他们较低层次的需要.在满足需要的过程中,学生不再为温饱而操心,他们有良好的家庭环境和社会环境,对自己的生活有基本的安全感,尤其是在他们的感情需要、友爱需要能得到充分满足的情况下他们会更倾向于发展求知、审美、创造、自信等宝贵的品质.相反,如果学生的基本心理需要得不到满足,缺乏基本的生活资料,生活在一个具有威胁的环境中,得不到爱,感受不到人于与之间的温暖,经常受到他人的排挤,他们会变得胆怯、退缩、敌意,从而也就丧失求知的欲望.所以数学课上,我们应给学生提供一个友善的,能使学生产生归属感的课堂环境来促进学生的学习.

三、精心选择,融入一些生动有趣的数学知识

在初中数学教学中,教师可结合学习内容讲述诸如数学发展简史、数学理论所经历的沧桑、数学家的成长过程和有关贡献、数学中某些结论的来历等以帮助学生理解和记忆数学知识.还可有的放矢地讲述一些趣味性强、容易使学生产生强烈好奇心和丰富想象力的数学典故,这样不仅活跃了课堂气氛,又令学生产生了愉快的学习心理,自然意兴盎然、其乐无穷.例如：“勾股定理”及其逆定理的应用是教学中的重点又是难点,学生普遍感到内容简单但很难灵活运用.于是我首先介绍中国古代著名数学著作《周髀算经》中关于勾股定理内容的著名叙述,即“勾三、股四、弦五”,接着又列举并解答了《九章算术》中记载的一个关于勾股定理应用的实际问题,让学生在钦佩古人数学钻研精神的同时,对中国古代数学成就倍感自豪,继而克服因“畏难”而造成的学习困难.

四、重视培养学生的内部动机

我们的教育往往比较重视培养学生的外部学习动机.例如我们多数教师都喜欢通过分数、奖励、荣誉等激发学生的学习动机.但当代教育有一种越来越重视内部动机的倾向.因为内部动机才能真正使整个学习过程变得富有吸引力,使整个学习过程都充满激励性.重视内部动机,也就是要重视知识本身的兴趣,使学生发自内心地热爱知识,而不是单纯地把学习知识当成获得某种报酬的手段.学生形成了良好的内部动机,学习就成了人的精神需要,学习行为就成了自觉、自愿的过程.在这样的学习模式下,学习效果定能显著提高.

五、实现教学民主,放飞心灵翅膀

课堂是学生成长的土壤,民主和谐的氛围是催生学生健康成长的阳光雨露.只有民主和谐的课堂氛围,才有利于促进学生自主、探究、合作学习,实现学习方式的根本转变.在民主化,生活化的课堂中,教师要具有诚挚的态度与爱心,有与学生平等相处的心态,要尊重学生,宽容学生,使学生觉得师生是朋友、伙伴.课堂的民主性不仅体现在师生关系的情感和谐上,而且还应体现在对教与学关系的矛盾处理中,使学生以宽松的心态,自主的思维,亲历认知过程,让学生因能主动获取知识与技能而对学习充满自信.而在这一点上,过去不为大家所重视.常出现师生关系民主而在授知上是专制的,学生情绪放松而思维却禁锢.在教学中数学教师要不断探索如何做到解放学生的口,解放学生的手,解放学生的脑,放飞学生心灵的翅膀,使课堂教学体现真正的民主性.

总之,数学教师在教学中应不断探索教育教学规律,培养学生的学习兴趣,提高教学质量.