欢迎您访问52IJ教育培训网，今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的：“三角形三边求面积_...将此三角形旋转一周，求所得到的旋转体的表面积和...[数学]”，注意：所整理内容不代表本站观点，如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
本文发布时间:2016-04-21 14:15 编辑:勤奋者
精选知识
AC×BC
∴OC=2.4，
∴旋转体的体积=两个圆锥体积和=
×π×2.42×AB=
旋转体的表面积=
×2π×2.4×（3+4）=
AC×BC
∴OC=2.4，
∴旋转体的体积=两个圆锥体积和=
×π×2.42×AB=
旋转体的表面积=
×2π×2.4×（3+4）=
=
×3.14×49×3
=153.86（立方厘米）；
答：这个圆锥的体积是153.86立方厘米．
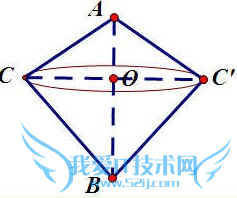如图，旋转后图形的轴截面是四边形ACBC'，
连结CC'交AB于O，则CC'⊥AB
∵AC=3，BC=4，AB=5
∴AB2=AC2+BC2，
∴△ABC是直角三角形，
∴S△ABC=1 2
| 1 |
| 2 |
∴OC=2.4，
∴旋转体的体积=两个圆锥体积和=
| 1 |
| 3 |
| 48π |
| 5 |
旋转体的表面积=
| 1 |
| 2 |
| 84π |
| 5 |
其他类似问题
问题1：Rt△ABC的三边长分别是AC=3，BC=4，AB=5，以AB所在直线为轴，将此三角形旋转一周，求所得到的旋转体的表面积和体积．[数学科目]
如图，旋转后图形的轴截面是四边形ACBC'，
连结CC'交AB于O，则CC'⊥AB
∵AC=3，BC=4，AB=5
∴AB2=AC2+BC2，
∴△ABC是直角三角形，
∴S△ABC=1 2
| 1 |
| 2 |
∴OC=2.4，
∴旋转体的体积=两个圆锥体积和=
| 1 |
| 3 |
| 48π |
| 5 |
旋转体的表面积=
| 1 |
| 2 |
| 84π |
| 5 |
问题2：如图梯形ABCD中,AB平行CD,AC,BC交于点E,若三角形DCE的面积:三角形DCB的面积=1:3,求三角形的面积DCE:S三角[数学科目]
∵S△DCE：S△DCB=1：3,
∴DE：BD=1：3,
即DE：BE=1：2,
∵CD‖AB,
∴ DE:BE=CE:AE=1/2 ,
∴S△DCE：S△AED=1：2,S△DCE：S△ABE=1：4,
∴S△DCE：S△ABD=1：6．
问题3：如图,三角形ABC中,角BAC=30°,AC=2a,BC=b,以直线AB为轴旋转一周,求这个旋转体的表面积[数学科目]
过C作CD⊥AB交AB于D
∵∠BAC=30°
∴CD = 1/2 AC = a
以直线AB为轴旋转一周的表面积,
就得以CD为底面半径,分别以AC、BC为母线的两个圆锥的侧面积之和
1/2 ×2π * a×b + 1/2 ×2π * a×2a
＝（2a^2 + ab）π
问题4：如图把三角形ABC以AB为轴旋转一周得到一个图形，求这个图形的体积？单位：厘米[数学科目]
1 3
=
| 1 |
| 3 |
=153.86（立方厘米）；
答：这个圆锥的体积是153.86立方厘米．
问题5：如图,已知三角形abc中,ac=4,bc=3,ab=5.现绕ac边所以的直线旋转一周,求旋转后的几何体的体积是多少?明天交的~如图,已知三角形abc中,ac=4,bc=3,ab=5.现绕ac边所以的直线旋转一周,求旋转后的几何体的[数学科目]
这是一个沿着直角三角形abc的直角边ac旋转的过程,获得的立体图形为圆锥：
体积为3^2π*4/3=12π
- 评论列表（网友评论仅供网友表达个人看法，并不表明本站同意其观点或证实其描述）
-