在四边形abcd中_19、在平行四边形ABCD中，E、F分别是AB、CD的中点，连接AF、CE.[数学]

精选知识

1、证明

∵平行四边形ABCD

∴AB＝CD,AD＝BC,∠B＝∠D

∵E是AB的中点

∴BE＝AB/2

∵F是CD的中点

∴DF＝CD/2

∴BE＝CF

∴△BEC≌△DFA

2、四边形AECF是矩形

证明：

∵E是AB的中点

∴AE＝BE

∵CA＝CB,CE＝CE

∴△ACE全等于△BCE

∴∠AEC＝∠BEC＝90

∴CE⊥AB

∵AD＝BC,BC＝AC

∴AC＝AD

∵F是CD的中点

∴CF＝DF

∵CE＝CE

∴△ACE全等于△BCE

∴∠AFC＝∠AFD＝90

∴AF⊥CD

∵AB∥CD

∴矩形AECD

其他回答

我知道更简单的！！！

其他类似问题

问题1：如图,ABCD为平行四边形,E、F分别为AB、CD的中点,①求证：AECF也是平行四边形；②连接BD,分别交CE、AF于G、H,求证：BG=DH；③连接CH、AG,则AGCH也是平行四边形吗?[数学科目]

❶：根据已知可知：AE∥FC且AE=FC AD=BC DF=EB ∠ABC=∠ADC

∴△ADF≌△CBE (SAS) ∴AF=CE ∠DAF=∠ECB

∴四边形AECF是平行四边形

❷：∵AD∥BC ∴∠ADH=∠CBG

∴有∠ADH=∠CBG ∠DAF=∠ECB AD=BC

∴△ADH≌△CBG(ASA)

∴DH=BG

❸：是平行四边形

∵DH=BG AD=BC ∠HDA=∠GBC

∴△AHD≌△CBG(ASA)

∴AH=CG

∴同理可证得CH=AG

∴四边形AGCH是平行四边形

问题2：已知:如图,在平行四边形ABCD中,点E,F在AC上,且AF=CE,点G,H分别在AB,CD上,且AG=CH,AC与GH相交于点O 求证⑴EG‖FH⑵GH,EF互相平分[数学科目]

（1）

∵四边形ABCD为平行四边形

∴AB∥CD

∴∠GAE=∠HCF

∵AF=CE

∴AE=AF-EF

    =CE-EF=CF

在△GAE和△HCF中

AG=CH

∠GAE=∠HCF

AE=CF

∴△GAE≌△HCF（SAS）

∴∠AEG=∠CFH

∴∠OEG=180°-∠AEG

    =180°-∠CFH=∠OFH

∴EG∥FH

 

（2）

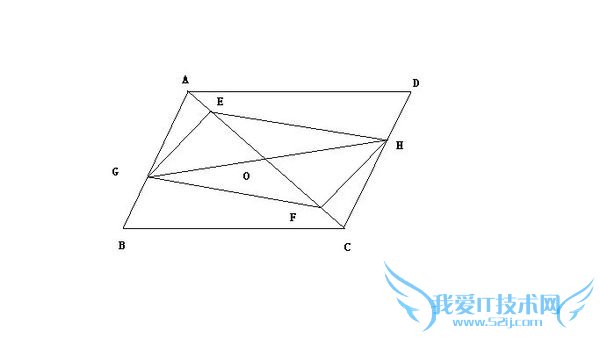
连接EH,FG

∵△GAE≌△HCF

∴EG=FH

∵EG∥FH

∴四边形EGFH为平行四边形

∴GH与EF相互平分

问题3：平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,CE与BF相交于点H什么时候EHFG是菱形?请证明.什么时候EHFG是正方形?请证明.

平行四边形ABCD,E,F分别是AB,CD的中点

AD=BC,∠DAE=∠BCD,AE=DF

三角形DAE≌三角形BCF

DE=BF

BE=CF

四边形BFDE是平行四边形

DE‖BF

同理可得：AF‖CE

四边形EHFG是平行四边形

1.当平行四边形ABCD是矩形时,平行四边形EHFG是菱形

四边形ABCD是矩形

∠ABC=∠DCB=90°,BE=CF,BC=BC

三角形EBC≌三角形FCB

CE=BF

∠ECB=∠FBC

BH=CH

EH=FG

平行四边形EHFG是菱形

2.当平行四边形ABCD是矩形,并且AB=2AD时,平行四边形EHFG是正方形

这时 AE=AD=DF=AB/2

∠EAD=∠FDA=90°

四边形ADFE是正方形

EG=FG=AF/2,AF⊥DE

∠EGF=90°

平行四边形EHFG是正方形.

问题4：如图,在平行四边形ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,CE与BF相交于点H.(1)图中除平行四边形ABCD外还有哪几个平行四边形?请说明理由.(2)如果四边形ABCD是矩形,则四边形EHFG将是一个什[数学科目]

解（1）：还有三个

∵E、F分别是AB、CD的中点

∴EB=AE=1/2AB DF=CF=1/2CD

∵四边形ABCD是平行四边形

∴AB平行于CD AB=CD

∴EB=AE=DF=CF

∵EB=DF EB平行于DF

∴四边形EBFD是平行四边形

又∵AE=CF AE平行于CF

∴四边形AECF是平行四边形

∵四边形EBFD是平行四边形且四边形AECF是平行四边形

∴EG平行于HF EH平行于GF

∴四边形EGFH是平行四边形

问题5：在?ABCD中，E、F分别是AB、CD的中点，连接AF、CE． （1）求证：△BEC≌△DFA；（2）连接AC，当CA=CB时，判断四边形AECF是什么特殊四边形？并证明你的结论．[数学科目]

（1）证明：∵四边形ABCD是平行四边形，
∴BC=AD，∠B=∠D，AB=CD，
∵E、F分别是AB、CD的中点，
∴BE=DF=AE=CF，
在△BEC和△DFA中，
BE=DF，∠B=∠D，BC=AD，
∴△BEC≌△DFA．
（2）答：四边形AECF是矩形．
证明：∵四边形ABCD是平行四边形，
∴AB∥CD，
∵AE=CF，
∴四边形AECF是平行四边形，
∵AC=BC，E是AB的中点，
∴CE⊥AB，
∴∠AEC=90°，
∴平行四边形AECF是矩形．