欢迎您访问52IJ教育培训网,今天小编为你分享的高考数学方面的学习知识是通过网络精心收集整理的:“5.1.1关闭验证_线性代数问题 求选项的正面证明设A是54矩阵,A=(a1,a...[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
由条件知A的秩是2,只需验证a2,a3线性无关即可
注意a1=2a3,a2=-a4,如果a2和a3线性相关,那么a1,a2,a3,a4的秩就是1,矛盾
其他类似问题
问题1:线性代数证明题习题最后有这样一道题,我根本看不懂啊,不知道让证明什么,望高人予以赐教.试证:n维向量空间V中任意k(1=[数学科目]
设a1,a2,...,ak是n维向量空间V中任意k个线性无关的向量,如果k
问题2:关于线性代数的证明问题,求教If the argumengted matrices of two linear systems are row equivalent,then the two systems have the same solution set.In other words,elementary row operations do not change solution set.elementary row operations
时间有限,大略说下.
假设原矩阵A各列有线性关系,记为(*):Ai=k1A1+k2A2+k3A3+...k(i-1)A(i-1)+k(i+1)A(i+1)+...+knAn,其中ki为系数,Ai表示A的各列
对A进行若干次初等行变换,实质上就是对A左乘一系列初等矩阵,这些初等矩阵的乘积可以看成一个可逆矩阵P,即
变换后的矩阵B=PA,将B和A按列分块,得到
[B1,B2,...,Bi-1,Bi,Bi+1,...,Bn]=P[A1,A2,...,Ai-1,Ai,Ai+1,...An]
则,Bi=PAi (i=1,2,...,n)
对于(*):Ai=k1A1+k2A2+k3A3+...k(i-1)A(i-1)+k(i+1)A(i+1)+...+knAn,统一左乘P,得到
PAi=k1PA1+k2PA2+k3PA3+...k(i-1)PA(i-1)+k(i+1)PA(i+1)+...+knPAn,
也就就是Bi=k1B1+k2B2+k3B3+...k(i-1)B(i-1)+k(i+1)B(i+1)+...+knBn,
上式说明经过初等行变换后,新矩阵的列之间的线性关系保持不变.
问题3:线性代数 证明题若矩阵A不可逆,则其伴随矩阵A*也不可逆.[数学科目]
A的为1阶方阵时A不可逆<=>A=0,所以A*=0,所以不可逆
A的阶数n大于等于2时
(A*)*=|A|^(n-2)A(证明见参考资料例6)
因为A不可逆所以|A|=0
所以(A*)*=O
所以A*(A*)*=|A*|E=0
所以|A*|=0,即,A*不可逆
问题4:线性代数的证明题,设向量β可由向量组α1,α2,…αS,线性表示,但不能由向量组(Ⅰ)α1,α2,…αS-1线性表示.记向量组(Ⅱ)α1,α2,…αS-1,β,试证向量αS不能由(Ⅰ)线性表示,但可以由(Ⅱ)线[数学科目]
证:(1)反证.
假如αs能由α1,α2,…αs-1线性表示
由已知β可由向量组α1,α2,…αs线性表示
所以 β可由向量组α1,α2,…αs-1线性表示
这与β不能由向量组α1,α2,…αs-1线性表示矛盾.
所以αs不能由α1,α2,…αs-1线性表示.
(2)由已知β可由向量组α1,α2,…αs线性表示,即有
β=k1α1+k2α2+…+ksαs.
再由已知β不能由向量组α1,α2,…αs-1线性表示
所以 ks≠0.
所以有 αs = β/ks-k1/ksα1-k2/ksα2-…-ks-1/ksαs-1
即αs可由α1,α2,…αs-1,β线性表示#
问题5:线性代数求教,这个要怎么证明?
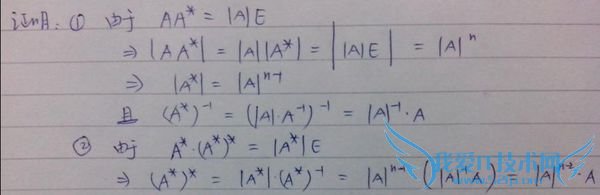
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
