欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“椭圆_已知椭圆 经过点 ,离心率为 .(1)求椭圆 的方程;(2)直...[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
已知椭圆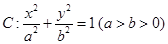 经过点
经过点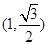 ,离心率为
,离心率为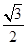 .
.
(1)求椭圆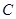 的方程;
的方程;
(2)直线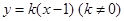 与椭圆
与椭圆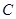 交于
交于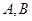 两点,点
两点,点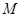 是椭圆
是椭圆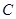 的右顶点.直线
的右顶点.直线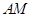 与直线
与直线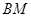 分别与
分别与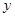 轴交于点
轴交于点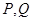 ,试问以线段
,试问以线段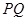 为直径的圆是否过
为直径的圆是否过![]() 轴上的定点?若是,求出定点坐标;若不是,说明理由. (1)椭圆
轴上的定点?若是,求出定点坐标;若不是,说明理由. (1)椭圆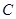 的方程是
的方程是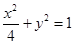 ;(2)线段
;(2)线段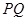 为直径的圆过
为直径的圆过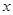 轴上的定点
轴上的定点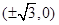 .
.
试题分析:(1)求椭圆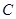 的方程,已知椭圆
的方程,已知椭圆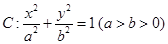 经过点
经过点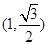 ,离心率为
,离心率为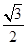 ,故可用待定系数法,利用离心率可得
,故可用待定系数法,利用离心率可得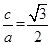 ,利用过点
,利用过点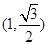 ,可得
,可得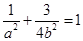 ,再由
,再由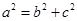 ,即可解出
,即可解出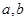 ,从而得椭圆
,从而得椭圆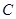 的方程;(2)这是探索性命题,可假设以线段
的方程;(2)这是探索性命题,可假设以线段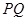 为直径的圆过
为直径的圆过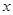 轴上的定点
轴上的定点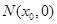 ,则
,则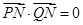 ,故需表示出
,故需表示出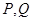 的坐标,因为点
的坐标,因为点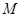 是椭圆
是椭圆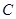 的右顶点,所以点
的右顶点,所以点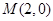 ,设
,设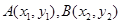 ,分别写出直线
,分别写出直线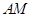 与的
与的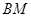 方程,得
方程,得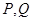 的坐标,由
的坐标,由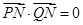 ,得
,得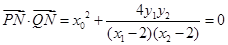 ,因此由
,因此由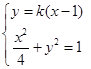 得
得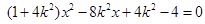 ,则
,则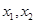 式方程的根,利用根与系数关系得,
式方程的根,利用根与系数关系得,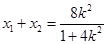 ,
,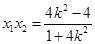 ,代入
,代入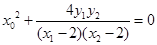 即可.
即可.
试题解析:(1)由题意得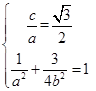 ,解得
,解得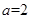 ,
,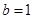 .
.
所以椭圆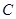 的方程是
的方程是
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
