同学们提问关于“二重积分的几何意义_二重积分的几何意义函数f(x,y)在区域D上连续且非负,...[数学]”的问题,52IJ师说平台通过网络上精心整理了以下关于“二重积分的几何意义_二重积分的几何意义函数f(x,y)在区域D上连续且非负,...[数学]”的一些有用参考答案。请注意:文中所谈及的内容不代表本站的真正观点,也请不要相信各种联系方式。下面是本网所整理的“二重积分的几何意义_二重积分的几何意义函数f(x,y)在区域D上连续且非负,...[数学]”的相关信息:
二重积分的几何意义函数f(x,y)在区域D上连续且非负,...
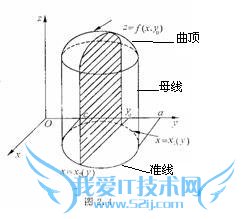
科目:数学 关键词:二重积分的几何意义圆柱知道吧,底下的圆就是准线,直线就是母线
其他类似问题
问题1:二重积分的几何意义:为什么?[数学科目]
楼上解释错了.
1、本题的被积函数是一个顶点在原点的圆锥体,不是圆柱体.
2、如果被积函数的量纲是长度单位,则二重积分为体积;
3、如果被积函数的量纲是Pa,则二重积分的意义为计算总压力;
4、如果被积函数的量纲是kg/m2,则二重积分的意义就是算总质量;
5、如果被积函数的量纲是C/m2 ,则二重积分的意义就是算总电量;
、、、、、、
结论:
1、二重积分是否有意义,要看被积函数的量纲,由量纲决定是否有物理意义.
2、数学老师出题,一般不会考虑什么物理模型、量纲,一般均无明确意义.
3、对于数学老师随意出出来的二重积分题,笼统地讲是算体积,其实是错的.
4、被积函数如果是1,而且这个1不带任何单位,那二重积分就是算总面积.
5、只要被积函数不是1,一般来说,二重积分没有明确意义,只是乱积而已.
数学老师出出来的二重积分的题,一般都是为了练习、熟练积分而出的题,
不必认真,只是练习而已.如果你一旦认真起来,无论你的天赋多高,创
造力多强,无论数学老师多烂,都会骂你“钻牛角尖”,“脑子有问题”.天才
就当成了白痴.
本题的解释:
1、因为本题的被积函数是圆锥体,假设x、y均有长度量纲,本题的被积函数
的意义是圆锥体上的任何一点,这一点到x-y平面的垂直高度;
2、这个高度乘以x-y平面上的微元面积dxdy,就是一个细高的立体体积,这个
细高立体的底面在x-y平面上,顶面在圆锥体的侧面上.
3、积分的结果就是圆锥体下方到x-y平面的立体体积.
4、这个体积正好等于以圆锥口为顶面,底面在x-y平面上的圆柱的体积,减去
圆锥的体积.也就是楼主题目所问的问题.
5、本题是特例,结果等于圆柱的体积减去圆锥的体积.一般情况下不是这样.
问题2:二重积分的几何意义是什么[数学科目]
当被积函数在积分区域内是正数是,几何意义是积分曲面与投影面所围区域的体积,若有正有负则是正的区域部分体积减去负的区域部分的体积
问题3:二重积分的几何含义是体积,但是二重积分可以积出负数,[数学科目]
二重积分的几何意义
当被积函数大于零时,二重积分是柱体的体积
当被积函数小于零时,二重积分是柱体的体积的负值.
具体
http://nhjy.hzau.edu.cn/kech/wjf/dzja/duomeiti7/71/12.htm
问题4:二重积分问题,有关二重积分的几何意义的,请问∫∫dxdy与∫∫ds在某曲面E上的二重积分分别有什么几何意义(被积函数都是1),希望能说的详细些,[数学科目]
这有什么几何意义,很简单啊,你被积函数都是1,求的不就是被积分区域的平面和曲面面积吗?
详细说,dxdy就是平面的微小面积元,二重积分就是把这些微小面积元全累加,不过是一个分的越来越细,加的越来越准的极限过程,本质上讲就是对面积元求和(因为被积函数是1),所以求出来的就是积分区域面积萨.曲面完全类似,就是用曲面的微小面积元代替平面的而已.
问题5:利用二重积分的几何意义计算二重积分.∫∫Sqrt(1-x^2-y^2)dσ,D:x^2+y^2≤1[数学科目]
上式的几何意义是球x^2+y^2+z^2=1的上半球的体积(0
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
