f0≠0，f1=12，f(a +b)=fafb，f(-2)等于多少

精选知识

f(0+1)=f(0)f(1)=1/2f(0),所以f(0)=1,

f（2)=f(1)f(1)=1/4,

f(0)=f(2)f(-2)=1,

f(-2)=4

其他回答

令a=b=0,则f(0)=f(0)f(0),因f(0)不为0，所以有f(0)=1

令a=b=1,则f(1+1)=f(1)f(1),得：f(2)=f(1)^2=1/4

令a=2, b=-2,则f(2-2)=f(2)f(-2),即1=1/4* f(-2)

所以f(-2)=4

其他类似问题

问题1：设函数f0(x)＝(12)|x|，f1(x)＝|f0(x)?12|，fn(x)＝|fn?1(x)?(12)n|，n≥1，n∈N，则方程fn(x)＝(1n+2)n有______个实数根．[数学科目]

先令n=1，则有：|f₀（x）-12

|=13

，∴

(12)

|x|

＝56

或16

，可知有2²=4个根；
于是当n=k+1时，会有f_k+1（x）=±[f_k（x）-(12

)

k

]=(1k+1+2

)

k+1

，依此类推，每个方程去掉绝对值符号，都对应两个方程，而每个方程又会有两个根，从而可以得到有2ⁿ⁺¹个根．
故答案为：2ⁿ⁺¹．

问题2：设f0（x）=sinx，f1（x）=f0′（x），f2（x）=f1′（x），…，fn+1（x）=fn′（x），n∈N，则f2005（x）=（　　）A. sinxB. -sinxC. cosxD. -cosx[数学科目]

f₀（x）=sinx，f₁（x）=f₀′（x）=cosx，f₂（x）=f₁′（x）=-sinx，
f₃（x）=f₂′（x）=-cosx，f₄（x）=f₃′（x）=sinx，循环了
则f₂₀₀₅（x）=f₁（x）=cosx，
故选C．

问题3：以知指数函数fx=a^x(a>=0且a不等于0)的图像经过(3,兀)求f0,f1,f-3.[数学科目]

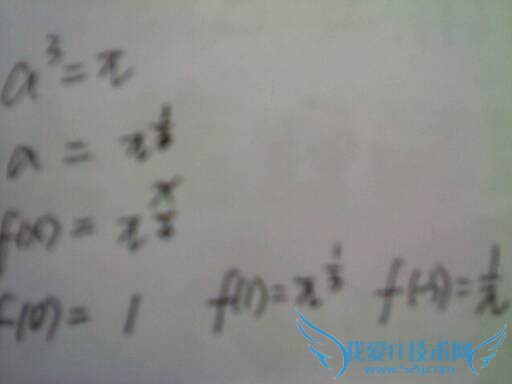
问题4：已知二次函数fx满足f(1+x)=f(1-x),且f0=0,f1=1,若fx在区间[m,n]上的值域是,则见图!鼠标左键点击放大！[数学科目]

已知二次函数f(x)满足f(1+x)=f(1-x),且f(0)=0,f(1)=1 ,

若函数f(x)在区间[m,n]的值域为[m,n],则m=___,n=____.

由f(1+x)=f(1-x)知二次函数f(x)的图象的对称轴为直线x=1

又∵过点(1,1),(0,0),∴点(1,1)是函数图象的顶点,可设f(x)=a(x-1)^2+1

∴a+1=0,∴a=-1.∴f(x)=-(x-1)^2+1=-x^2+2x

∵函数f(x)在区间[m,n]的值域为[m,n],所以n≤1

∴函数f(x)在区间[m,n]上是增函数.

∴-m^2+2m=m且m

问题5：f0(x)=xe^x,f1(x)=f0'(x),f2(x)=f1'(x),.,fn(x)=f'n-1(x)(n∈N^*),f2012(0)=?[数学科目]

2012e^x +xe^x