积分∫(2r){(x^2+r^2)^(32)} dr求完全具体步骤!∫(...

精选知识

∫(2r)/{(x^2+r^2)^(3/2)} dr

=∫(x^2+r^2)^(-3/2) dr^2

=∫(x^2+r^2)^(-3/2) d(x^2+r^2)

=(x^2+r^2)^(-3/2+1)/(-3/2+1)+C

=-2(x^2+r^2)^(-1/2)+C

=-2/√(x^2+r^2)+C

其他类似问题

问题1：求积分：∫（r^3/(r^2+x^2)）dr 问错了。分母上还有个二分之三次方~∫（r^3/(r^2+x^2)^(3/2)）dr[数学科目]

∫r3/(r2+x2)^(3/2) dr

令u=r2+x2

du=2r dr

原式=(1/2)∫(u-x2)/u^(3/2) du

=(1/2)∫[1/√u - x2/u^(3/2)] du

=(1/2)[2√u + 2x2/√u] + C

=√u + x2/√u + C

=(u+x2)/√u + C

=(r2+2x2)/√(r2+x2) + C

问题2：求积分∫(0,a)r/√(x^2+r^2)dr[数学科目]

解题关键：积分过程中吧x做常数处理,第二类换元积分法.

满意请采纳!

问题3：三角函数方程组 sin(x)*r=0.3 2r+cos(x)2r=1 求r的值[数学科目]

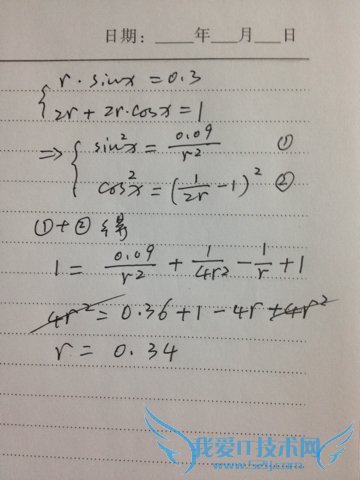
问题4：关于高数二重积分,为什么在S范围内积分,S:(x-R)^2+y^2+z^2=R^2,积分式为∫∫2R(x-R)dS=0?[数学科目]

做一个变换 u=x-R 则 S:u^2+y^2+z^2=R^2

积分为 ∫∫2R u dS = 2R∫∫ u dS

然后由对称性可知结果为0.

问题5：(x/3+3/√x)^9的式常数项：=C(r,9)*(x/3)^(9-r)*(3/√x)^r =C(r,9)*3^(2r-9)*x(9-3r/2)(x/3)^(9-r)是怎样变成3^(2r-9)(3/√x)^r是怎样变成x(9-3r/2)[数学科目]

你理解错了

它是把系数作系数处理,韦知数x单独拿开处理

C(r,9)*(x/3)^(9-r)*(3/√x)^r=C(r,9)*3^(2r-9)*x(9-3r/2)

其中含x的有x^(9-r)*x^(-r/2)=x^(9-3r/2)

系数是C(r,9)*(1/3)^(9-r)*3^r=C(r,9)*3^(2r-9)