欢迎您访问52IJ教育培训网，今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的：“mc冰吻_...A，C在一直线上，连接BD，取BD的中点M，连ME，MC试判断...[数学]”，注意：所整理内容不代表本站观点，如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
三角形EMC为等腰直角三角形.
证明如下：
已知三角形ADE和三角形ABC为两个全等的含30度,60度角直角三角形
则角DEA=角ACB=90° 角EDA=角BAC=60° 角DAE=角ABC=30°
所以 角DAB=90°又有AD=AB
所以三角形DAB为等腰直角三角形
角ADB=45°
DM=MA=MB
因为M为BD边的中点M
所以AM为三角形DAB BD边的高
可得 角MAB=45°=角ADB
角ADB=45°三角形DMA为等腰直角三角形
DM=MA=MB
所以角EDM=角MAC=45°+60°=105°
又 ED=AC
三角形MDE与三角形MAC全等
所以ME=MC 角DEM=角MCA
三角MEC为等腰三角形
角MEC=角MCE
所以 角DEM=角MEC=角MCE=45°
可得 角EMC=90°
即三角MEC为等腰直角三角形
其他回答
2011-10-15 20:24 热心网友 三角形EMC为等腰直角三角形。
证明如下：
已知三角形ADE和三角形ABC为两个全等的含30度，60度角直角三角形
则角DEA=角ACB=90° 角EDA=角BAC=60° 角DAE=角ABC=30°
所以 角DAB=90°又有AD=AB
所以三角形DAB为等腰直角三角形
角ADB=45°
DM=...
其他类似问题
问题1：两个全等的含30°，60°角的三角板ADE和三角板ABC如图所示放置，E，A，C三点在一条直线上，连接BD，取BD的中点M，连接ME，MC．试判断△EMC的形状，并说明理由．[数学科目]
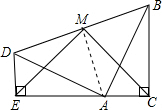△EMC是等腰直角三角形．理由如下：
连接MA．
∵∠EAD=30°，∠BAC=60°，
∴∠DAB=90°，
∵△EDA≌△CAB，
∴DA=AB，ED=AC，
∴△DAB是等腰直角三角形．
又∵M为BD的中点，
∴∠MDA=∠MBA=45°，AM⊥BD（三线合一），
AM=12
∴∠EDM=∠MAC=105°，
在△MDE和△CAM中，
ED=AC，∠MDE=∠CAM，MD=AM
∴△MDE≌△MAC．
∴∠DME=∠AMC，ME=MC，
又∵∠DMA=90°，
∴∠EMC=∠EMA+∠AMC=∠EMA+∠DME=∠DMA=90°．
∴△MEC是等腰直角三角形．
问题2：两个全等的含30度,60度角的三角板ADE和三角板ABC,按如图所放,E,A,C,三点在一天直线上,连接BD,取BD的两个全等的含30度，60度角的三角板ADE和三角板ABC，按如图所放，E,A,C,三点在一天直线上，连[数学科目]
证明：
∵∠EAD=∠ABC=30 or 60
∴∠BAD=90
AD=AB
∴AM⊥BD
∴四边形ACBM中,∠MAC+∠DBC=180
又∵M为BD中点,
∴MA=MB=MD
△DEM 和 △ACM中
∵DE=AC
又∵梯形BCDE中,∠EDB+∠DBC=180
∴∠EDB=∠MAC
综合 DE=AC DM=MA
∴△DEM≌△ACM
问题3：两个全等的含30°，60°角的三角板ADE和三角板ABC如图所示放置，E，A，C三点在一条直线上，连接BD，取BD的中点M，连接ME，MC．试判断△EMC的形状，并说明理由．[数学科目]
△EMC是等腰直角三角形．理由如下：
连接MA．
∵∠EAD=30°，∠BAC=60°，
∴∠DAB=90°，
∵△EDA≌△CAB，
∴DA=AB，ED=AC，
∴△DAB是等腰直角三角形．
又∵M为BD的中点，
∴∠MDA=∠MBA=45°，AM⊥BD（三线合一），
AM=12
∴∠EDM=∠MAC=105°，
在△MDE和△CAM中，
ED=AC，∠MDE=∠CAM，MD=AM
∴△MDE≌△MAC．
∴∠DME=∠AMC，ME=MC，
又∵∠DMA=90°，
∴∠EMC=∠EMA+∠AMC=∠EMA+∠DME=∠DMA=90°．
∴△MEC是等腰直角三角形．
问题4：两个全等的含30°，60°角的三角板ADE和三角板ABC如图所示放置，E，A，C三点在一条直线上，连接BD，取BD的中点M，连接ME，MC．试判断△EMC的形状，并说明理由．[数学科目]
△EMC是等腰直角三角形．理由如下：
连接MA．
∵∠EAD=30°，∠BAC=60°，
∴∠DAB=90°，
∵△EDA≌△CAB，
∴DA=AB，ED=AC，
∴△DAB是等腰直角三角形．
又∵M为BD的中点，
∴∠MDA=∠MBA=45°，AM⊥BD（三线合一），
AM=12
∴∠EDM=∠MAC=105°，
在△MDE和△CAM中，
ED=AC，∠MDE=∠CAM，MD=AM
∴△MDE≌△MAC．
∴∠DME=∠AMC，ME=MC，
又∵∠DMA=90°，
∴∠EMC=∠EMA+∠AMC=∠EMA+∠DME=∠DMA=90°．
∴△MEC是等腰直角三角形．
问题5：两个全等的汉30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的重点M,连接ME,MC,试判断三角形EMC的形状,并说明理由!我实在说不出理由..答案应该是正三角形取B
那个,首先你的判断就是错的,应该是等腰直角三角形.
连接MA
∵∠EAD＝30°,∠BAC=60°
∴∠DAB=90°
∵△EDA≌△CAB
∴DA=AB,ED=AC,
∴△DAB是直角三角形
∴∠MDA=∠MAB=45°,AM⊥BD(三线合一）
AM=1/2BD=MD
∴∠EDM=∠MAC
在△MDE和△CAM中
ED=AC,∠MDE=∠CAM,MD=AM
∴△MDE≌△CAM
∴∠DME=∠AMC,ME=MC
又∵∠DMA=90°
∴∠EMC=∠EMA＋∠AMC=∠EMA＋∠DME=∠DMA＝90°
∴△MEC是等腰直角三角形
- 评论列表（网友评论仅供网友表达个人看法，并不表明本站同意其观点或证实其描述）
-