f x和gx分别是一个奇函数和一个偶函数，若 f x-gx=(1...

精选知识

设x=-x

所以-fx-gx=2^x

与f x-gx=(1/2)^x联立

解得fx=-(1/2^x-2^x)/2

gx=-(1/2^x+2^x)/2

把f(1),g(0),g(-2)代入

分别得 3/4 ,-1, -17/8

所以f(1)>g(0)>g(-2)

其他回答

从小到大的顺序是 g(-2),g(0),f(1)

解释如下：

由 f(0)= f(-0）= -f(0) 知 f(0)=0 从而g(0)=-1

由 f(1)=g(1)+1/2 及 -f(1)=f(-1)=g(1)+2 可以算出 f(1)=-3/4

由 f(2)=g(-2)+1/4 及 -f(2)=f(-2)=g(-2)+4 可以算出 g(-2)=-17/8

其他类似问题

问题1：设fx是偶函数,gx是奇函数,且fx+gx=1/(x-1),求fx,gx的解析式[数学科目]

由于f(x)+g(x)=1/(x-1) （1）

f(-x)+g(-x)=1/(-x-1) （2）

f(x)是偶函数,所以f(-x)=f(x)

g(x)是奇函数,所以g(-x)=-g(x)

所以（2）式变成f(x)-g(x)=-1/(x+1) （3）

(1)+(3)得f(x)=1/(x^2-1)

把它代入（1）得到g(x)=1/(x-1)-1/(x^2-1)=x/(x^2-1)

问题2：已知fx是奇函数,gx是偶函数且fx-gx=1/（x+1）求fx和gx已知函数fx=x(1/x2-1 +1/2),①求fx的定义域②判断函数fx的奇偶性并证明结论 跪求求求求求求[数学科目]

（1）∵ f（x）是奇函数,g（x）是偶函数

∴ f（- x）= - f（x）,g（- x）= g（x）

∵ f（x）- g（x）= 1 / （x + 1） ①

∴ f（- x）- g（- x）= 1 /（1 - x）

- f（x）- g（x）= 1 / （1 - x）

f（x）+ g（x）= 1 / （x - 1） ②

① + ② 得：

2 f（x）= 1 / （x + 1） + 1 / （x - 1）

= （x - 1） /（x + 1）（x - 1）+ （x + 1）/（x + 1）（x - 1）

= （x - 1 + x + 1）/ （x + 1）（x - 1）

= 2 x /（x 2 - 1）

∴f（x）= x / （x 2 - 1）

代入 ② 得：x / （x 2 - 1）+ g（x）= 1 / （x - 1）

∴ g（x）= 1 / （x - 1）- x /（x 2 - 1）

= （x + 1）/（x + 1）（x - 1）- x /（x + 1）（x - 1）

= （x + 1 - x）/（x + 1）（x - 1）

= 1 / （x 2 - 1）

∴ f（x）= x / （x 2 - 1） ,g（x）= 1 / （x 2 - 1）

（2）① ∵ f（x） = x【 1 / （x 2 - 1） + 1 / 2 】

∴ x 2 - 1 ≠ 0

x 2 ≠ 1

x ≠ ± 1

∴ 定义域为：｛x丨x ≠ ± 1｝

② f（x）是奇函数

证明：∵ f（- x）= - x 【 1 / （（- x） 2 - 1）+ 1 / 2 】

= - x 【 1 / （x 2 - 1）+ 1 / 2 】

= - f（x）

又∵ f（0）= 0 （1 / （0 2 - 1）+ 1 / 2 ） = 0

∴ f（x）是奇函数

问题3：若定义在r上的偶函数f(x) 和奇函数g(x)满足fx+gx=x2+3x+1 则fx[数学科目]

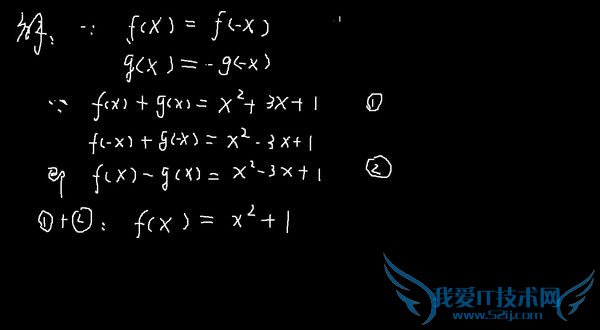
问题4：设函数f（x）与g（x）的定义域是x∈R且x≠±1，f（x）是偶函数，g（x）是奇函数，且f（x）+g（x）=1x?1．求：f（x）和g（x）的解析式．[数学科目]

∵f（x）是偶函数，g（x）是奇函数，∴f（-x）=f（x），且g（-x）=-g（x）
由f(x)+g(x)＝1x?1

①
得f(?x)+g(?x)＝1?x?1

，
即f(x)?g(x)＝1?x?1＝?1x+1

②
联立①②解得：f(x)＝1

x

2

?1

，g(x)＝x

x

2

?1

．

问题5：已知f（x）是偶函数，g（x）是奇函数，且f（x）+g（x）=（x2+1）（x+1），求f（x），g（x）的解析式．[数学科目]

因为f（x）是偶函数，g（x）是奇函数，
所以f（-x）=f（x），g（-x）=-g（x）
又因为f（x）+g（x）=（x²+1）（x+1），
所以f（-x）+g（-x）=f（x）-g（x）=[（-x）²+1]（-x+1）=（x²+1）（-x+1），
解得：f（x）=x²+1，g（x）=x（x²+1）．