点开来仔细看这是百度抽风的问题...与我无关

精选知识

9题

证：连接OM ,ON

因为N,M分别为AB,CD中点

所以OM垂直于AB,ON垂直于CD

所以∠OMA=∠ONC=90°

因为AB=CD

所以OM=ON

所以∠OMN=∠ONM

所以∠AMN=90°-∠OMN ,∠CNM=90°-∠ONM

因为∠OMN=∠ONM

所以∠AMN=∠CNM

10题

因为BC弧=DE弧

所以BC=DE

做OM垂直于BC,ON垂直于DE

因为弦BC=DE

所以OM平分BC,ON平分DE,∠OMA=∠ONA=90°,OM=ON

在△OMA和△ONA中

OM=ON

∠OMA=∠ONA=90°

OA=OA

所以△OMA全等△ONA

所以AM=AN

因为OM平分BC,ON平分DE

所以CM=EN

所以CM+AM=EN+AN

所以AC=AE

11题

连接OE ,EC

因为D为OC中点

由全等三角形可证得△OEC为等腰三角形

因为D为OC中点

所以OD=1/2*OC

所以OD=1/2*OE

所以∠OED=30°

所以∠DOE=180°-30°-90°=60°

因为CO垂直于AB,

所以∠COA=90°

所以∠EOA=90°-60°=30°

所以∠EOC=2∠AOE

所以EC弧=2EA弧

其他回答

你的题怎么这么多

其他类似问题

问题1：1.如图所示,AB=AC,AB为圆O的直径,AC、BC分别叫圆O于E、D,连结ED、BE,（1）试判断DE与BD是否相等,并说明理由：（2）如果BC=6,AB=5,求BE的长.2.如图,AB为圆O的直径,PQ切圆Q于T,AC垂直于PQ与C,交圆O于D（1)

1.分析：1）可通过连接AD,AD就是等腰三角形ABC底边上的高,根据等腰三角形三线合一的特点,可得出∠CAD=∠BAD,根据圆周角定理即可得出∠DEB=∠DBE,便可证得DE=DB．

（2）本题中由于BE⊥AC,那么BE就是三角形ABC中AC边上的高,可用面积的不同表示方法得出AC?BE=CB?AD．进而求出BE的长．

2.（1）DE=BD

证明：连接AD,则AD⊥BC

在等腰三角形ABC中,AD⊥BC

∴∠CAD=∠BAD（等腰三角形三线合一）

∵∠CAD=∠DBE,∠BAD=∠DEB

∴∠DEB=∠DBE

∴DE=BD；

（2）∵AB=5,BD= BC=3

∴AD=4 （1）DE=BD

证明：连接AD,则AD⊥BC

在等腰三角形ABC中,AD⊥BC

∴∠CAD=∠BAD（等腰三角形三线合一）

∵∠CAD=∠DBE,∠BAD=∠DEB

∴∠DEB=∠DBE

∴DE=BD；

（2）∵AB=5,BD= BC=3

∴AD=4

∵AB=AC=5

∴AC?BE=CB?AD

∴BE=4.8．

∵AB=AC=5

∴AC?BE=CB?AD

∴BE=4.8．

第二题

证明：（1）连接OT；

∵PQ切⊙O于T,

∴OT⊥PQ,

又∵AC⊥PQ,

∴OT‖AC,

∴∠TAC=∠ATO；

又∵OT=OA,

∴∠ATO=∠OAT,

∴∠OAT=∠TAC,

即AT平分∠BAC．

（2）过点O作OM⊥AC于M,

∴AM=MD= =1；

又∠OTC=∠ACT=∠OMC=90°,

∴四边形OTCM为矩形,

∴OM=TC= ,

∴在Rt△AOM中,

；

即⊙O的半径为2．

问题2：如图，在△ABC中，∠BCA=90°，以BC为直径的⊙O交AB于点P，Q是AC的中点．判断直线PQ与⊙O的位置关系，并说明理由．[数学科目]

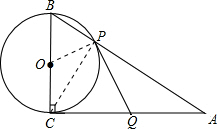直线PQ与⊙O的位置关系是：相切．
其理由如下：
①连接OP、CP．
∵BC是直径，
∴CP⊥AB，
在Rt△APC中，Q为斜边AC的中点；
∴PQ=CQ=12

AC（直角三角形斜边中线等于斜边一半），
∴∠QPC=∠QCP；
又OP=OC，
∴∠OPC=∠OCP，
又∠BCA=90°，
∴∠OPQ=90°，
∴OP⊥PQ，又∵OP为半径，
∴直线PQ与⊙O相切于点P．
②用三角形全等或者角的和（差）也可证明．

问题3：如图，已知O为原点，点A的坐标为（4，3），⊙A的半径为2．过A作直线l平行于x轴，交y轴于点B，点P在直线l上运动．（1）当点P在⊙A上时，请你直接写出它的坐标；（2）设点P的横坐标为12，[数学科目]

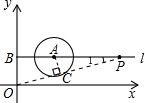（1）点P的坐标是（2，3）或（6，3）．
（2）连接OP，过点A作AC⊥OP，垂足为C．
那么AP=PB-AB=12-4=8，OB=3，
OP=

12

2

+

3

2

=153

．
∵∠ACP=∠OBP=90°，∠1=∠1，
∴△APC∽△OPB．
∴ACOB＝APOP

．
∴AC3＝8153

．
∴AC=24153

≈1.9＜2．
∴直线OP与⊙A相交．

问题4：关于圆的,越难越好,多一些[数学科目]

．在直径为AB的半圆内,划出一块三角形区域,如图所示,使三角形的一边为AB,顶点C在半圆圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形水池DEFN,其中D、E在AB上,如图24-94的设计方案是使AC=8,BC=6．

（1）求△ABC的边AB上的高h．

（2）设DN=x,且 ,当x取何值时,水池DEFN的面积最大?

（3）实际施工时,发现在AB上距B点1．85的M处有一棵大树,问：这棵大树是否位于最大矩形水池的边上?如果在,为了保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开大树．

分析：要求矩形的面积最大,先要列出面积表达式,再考虑最值的求法,初中阶段,尤其现学的知识,应用配方法求最值．（3）的设计要有新意,应用圆的对称性就能圆满解决此题．

（1）由AB?CG=AC?BC得h= =4.8

（2）∵h= 且DN=x

∴NF=

则S四边形DEFN=x? （4.8-x）=- x2+10x

=- （x2- x）

=- [（x- ）2- ]

=- （x-2.4）2+12

∵- （x-2.4）2≤0

∴- （x-2.4）2+12≤12 且当x=2.4时,取等号

∴当x=2.4时,SDEFN最大．

（3）当SDEFN最大时,x=2.4,此时,F为BC中点,在Rt△FEB中,EF=2.4,BF=3．

∴BE= =1.8

∵BM=1.85,∴BM>EB,即大树必位于欲修建的水池边上,应重新设计方案．

∵当x=2.4时,DE=5

∴AD=3.2,

由圆的对称性知满足条件的另一设计方案,如图所示:

此时,AC=6,BC=8,AD=1.8,BE=3.2,这样设计既满足条件,又避开大树．

问题5：初三数学题（关于圆）A,B,C为圆O上三点,D,E分别为弧AB,弧AC的中点,连DE分别交AB,AC于F,G,求证：AF=AG还没有学习到圆周角呢。。。[数学科目]

证明：

方法一：

连接AD、AE、BD、CE

因为D、E分别是弧AB、AC的中点

所以∠DAB＝∠B＝∠AED,∠ADE＝∠C＝∠CAE

而∠AFG＝∠ADE＋∠DAB,∠AGF＝∠CAE＋∠AED

所以∠AFG＝∠AGF

所以AF＝AG

方法二：

连接OD、OE,分别交AB、AC与P、Q

因为D、E分别是弧AB,AC的中点

所以OD⊥AB,OE⊥AC

所以∠APD＝∠AQE＝90°

因为OD=OE

所以∠ODE＝∠OED

因为∠DFP＝90°－∠D,∠EGQ＝90°－∠E

所以∠DFP＝∠EGQ

因为∠AFG＝∠DFP,∠AGF＝∠EGQ

所以∠AFG＝∠AGF

所以AF＝AG

虎年快乐～