萨达姆和卡扎菲_...斯大林，丘吉尔，毛泽东，萨达姆和卡扎菲下象棋，每两...[数学]

精选知识

2或3

其他类似问题

问题1：已知：在三角形ABC中,角CAB=2a.且a大于零度,小于30度,AP平分角CAB,P为三角形内部一点,连接AP,BP,CP.若角ABC=60--a,且角CBP=30度,求角APC（用含a的代数式表示）我表弟问我的……他寒假作业，[数学科目]

【题目】

已知在△ABC中,∠CAB=2α,且0＜α＜30°,AP平分∠CAB,若∠ABC=60°-α,点P在△ABC的内部,且使∠CBP=30°,求∠APC的度数（用含α的代数式表示）.

【解法一】

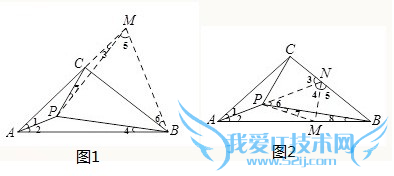
延长AC至M,使AM=AB,连接PM,BM（如图1）

∵AP平分∠CAB,∠CAB=2α

∴∠1=∠2= α

在△AMP和△ABP中：

∵AM=AB,∠1 =∠2,AP=AP

∴△AMP≌△ABP

∴PM=PB,∠3 =∠4

∵∠ABC=60°－α,∠CBP=30°

∴∠4=(60°－α)－30°=30°－α

∴∠3 =∠4 =30°－α

∵△AMB中,AM=AB

∴∠AMB=∠ABM=(180°－∠MAB)÷2 =(180°－2α)÷2 =90°－α

∴∠5=∠AMB－∠3= (90°－α)－(30°－α)=60°

∴△PMB为等边△

∵∠6=∠ABM－∠ABC = (90°－α)－(60°－α)=30°

∴∠6=∠CBP

∴BC平分∠PBM

∴BC垂直平分PM

∴CP=CM

∴∠7 =∠3 = 30°－α

∴∠ACP=∠7＋∠3=(30°－α)＋(30°－α)=60°－2α

∴△ACP中,∠APC=180°－∠1－∠ACP

=180°－α－(60°－2α)

=120°＋α

【解法二】

在AB上截取AM,使AM=AC,连接PM,延长AP交BC于N,连接MN（如图2）

∵AP平分∠CAB,∠CAB=2α

∴∠1=∠2=α

在△ACN和△AMN中：

∵AC=AM,∠1 =∠2, AN=AN

∴△ACN≌△AMN

∴∠3 =∠4

∵∠ABC=60°－α

∴∠3=∠2＋∠NBA=α＋(60°－α) =60°

∴∠3 =∠4 =60°

∴∠5=180°－∠3－∠4=180°－60°－60°=60°

∴∠4 =∠5

∴NM平分∠PNB

∵∠CBP=30°

∴∠6=∠3－∠NBP=60°－30°=30°

∴∠6=∠NBP

∴NP=NB

∴NM垂直平分PB

∴MP=MB

∴∠7 =∠8

∴∠6＋∠7 =∠NBP＋∠8

即∠NPM=∠NBM =60°－α

∴∠APM=180°－∠NPM =180°－(60°－α)=120°＋α

在△ACP和△AMP中：

∵AC=AM, ∠1 =∠2, AP=AP

∴△ACP≌△AMP

∴∠APC=∠APM

∴∠APC=120°＋α

问题2：如图,在等边三角形ABC中,点D,E,F分别在AB,BC,CA上,且角1=角2=角3,三角形DEF是等边三角形吗?试说明理由[数学科目]

∵在等边三角形ABC中

点D,E,F分别在AB,BC,CA上

∴DE=二分之一AC DF=二分之一BC EF=二分之一AB

∵AC=AB=BC

∴DE=DF=EF

∴三角形DEF是等边三角形

问题3：已知：以△ABC的边AB、AC、BC为边的等边三角形ABD、ACE、BCF求证：四边形ADFE是平行四边形[数学科目]

证明：∵∠ECF+∠ACF=60°

∠ACB+∠ACF=60°

∴∠ACB=∠ECF

∵在△ECF和△ACB中

∠ACB=∠ECF

AC=FC

BC=EC

∴△FCE≌△ACB

∴EF=AB

∵AB=AD

∴EF=AD

∵∠ABD-∠ABE=∠CBE-∠ABE

∴∠ABC=∠DBE

∵在△ABC和△DBE中

AB=BD

∠ABC=∠DBE

BC=BE

∴△ABC≌△DBE

∴AC=DE

∵AC=AF

∴AF=DE

又∵AD=EF

∴四边形DAEF是平行四边形

问题4：在△ABC中,AB=CB,∠ABC=90°,D是AB上一点,AE⊥CD交CD的延长线于点E,且AE=CD/2,BD=8cm,求点D到AC的距离[数学科目]

由△ADE相似于△BDC可得：AE/BC=AD/CD,得：（1/2）CD平方=BC*AD .设AB=CB=x,可得AD=x-8,CD的平方=64+x平方.带入（1/2）CD平方=BC*AD可得：

1/2（64+x平方）=x(x-8),化简为：x平方-16x-64=0,用求根公式求得x=8+8又根号2（另一根舍去）,故AD=x-8=8又根号2,由AB=CB,∠ABC=90°可知∠DAC=45°,故点D到AC的距离=AD/根号2=8.

问题5：在△ABC中，AB=AC，D是底边BC上一点，E是线段AD上一点，且∠BED=2∠CED=∠BAC．（1）如图1，若∠BAC=90°，猜想DB与DC的数量关系为______；（2）如图2，若∠BAC=60°，猜想DB与DC的数量关系，并证明你[数学科目]

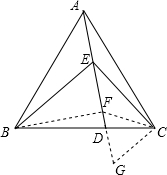（1）猜想：DB=2DC；
（2）在AD上截取AF=BE，连接CF，作CG∥BE交直线AD于G，
∵∠BED=∠BAC，
∴∠FAC=∠ABE，
∵在△ACF和△BAE中，CA＝AB∠AFC＝∠AEBAF＝BE

，
∴△ACF≌△BAE（SAS），
∴CF=AE，∠ACF=∠BAE，∠AFC=∠AEB．
∵∠ACF=∠BAE，∠AFC=∠BEA，
∴∠CFG=180°-∠AFC=180°-∠BEA=∠BED，
∵CG∥BE，
∴∠CGF=∠BED，
∴∠CFG=∠CGF，
∴CG=CF，
∵∠BED=2∠DEC，
∵∠CFG=∠DEC+∠ECF，∠CFG=∠BED，
∴∠ECF=∠DEC，
∴CF=EF，
∴BE=AF=2CF，
∵CG∥BE，
∴BD：CD=BE：CG，
∴BD：CD=2CF：CF=2，
∴BD=2DC，
∴BD与CD的数量关系与∠BAC的度数无关；
（3）∵BD与CD的数量关系与∠BAC的度数无关，
∴若∠BAC=α，那么（2）中的结论仍然还成立．